Chapter 6: The Curled Dimensions

In the previous two volumes, we established the universe’s macroscopic skeleton (relativity) and microscopic engine (QCA). In that picture, matter seems simple—it is just a projection of that constantly rotating vector onto the “internal sector” ($v_{int}$).

But as soon as we glance at the real world, we find this description too simplistic. The material world is not just a single “mass”; it is full of dazzling diversity: quarks, leptons, gluons, photons, W bosons… They possess various strange quantum numbers like charge, color charge, spin, isospin.

If the universe truly has only one vector, if $c_{FS}$ is truly the only budget, then where does this myriad splendor (The Ten Thousand Things) come from?

The answer lies in Recursion.

This chapter will reveal that $v_{int}$ is by no means the end; it is merely an entrance to a deeper geometric maze.

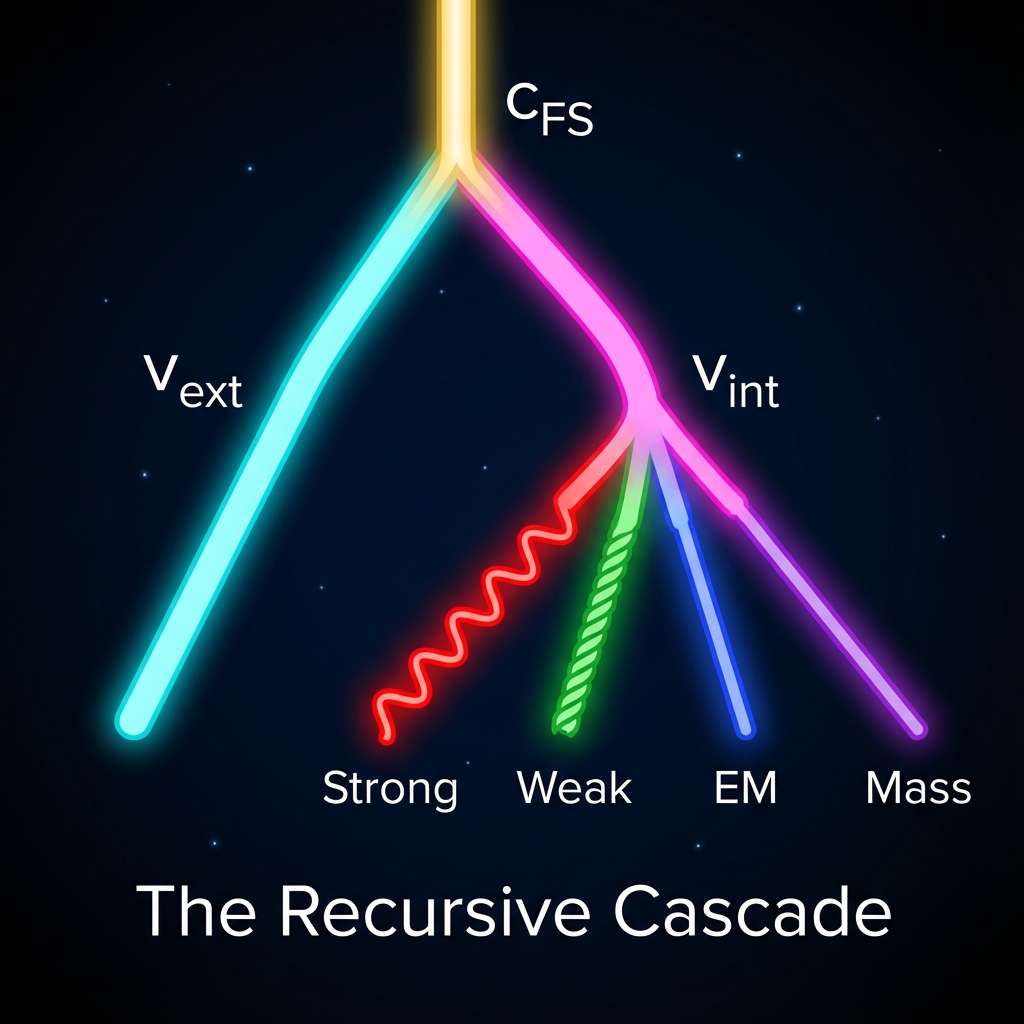
6.1 The Recursive Cascade

“The Tao gives birth to one, one gives birth to two, two gives birth to three, three gives birth to all things. This is not just philosophy; this is the computational logic of the universe’s underlying structure.”

In Volume 1, we performed the First Orthogonal Decomposition:

$$c_{FS}^2=v_{ext}^2+v_{int}^2$$

This created the binary opposition between spacetime and matter. For a particle that merely has mass, this might be sufficient. But in real physics, the “internal” is far more complex.

Internal is Not a Scalar, but a Manifold

When we say an electron has $v_{int}$, we are not just saying it “has mass.” The electron also carries charge and spin. This means that $v_{int}$ is not actually a simple scalar value but the magnitude of a multidimensional vector.

In the geometry of projective Hilbert space, the so-called “internal sector” is actually an extremely rich high-dimensional manifold. That vector representing the electron is not stationary in this manifold but is performing complex composite rotations.

To describe this complexity, we must introduce the Second Orthogonal Decomposition, and even the third and fourth.

The Cascade Pythagorean Theorem

Let us point our microscope at $v_{int}$. We discover that this component itself can be further decomposed into finer orthogonal subspaces.

According to the Standard Model’s symmetry group $SU(3)\times SU(2)\times U(1)$, we can expand the internal velocity budget $v_{int}$ into the following Cascade Identity:

$$v_{int}^2=v_{mass}^2+v_{gauge}^2$$

$$v_{gauge}^2=v_{strong}^2+v_{weak}^2+v_{em}^2$$

Combined, we obtain a more grand cosmic budget sheet:

$$c_{FS}^2=v_{ext}^2+\underset{\text{originally vague }{v}_{int}^2}{\underbrace{v_{mass}^2+v_{strong}^2+v_{weak}^2+v_{em}^2}}+v_{env}^2$$

This formula reveals the geometric essence of physics grand unification:

All forces (strong, weak, electromagnetic) and all material properties (mass) are essentially projections of the same vector onto different internal dimensions.

• Electromagnetic force ($v_{em}$): The rotation speed of the vector in the $U(1)$ subspace (circle).

• Weak interaction ($v_{weak}$): The rotation speed of the vector in the $SU(2)$ subspace (three-sphere).

• Strong interaction ($v_{strong}$): The complex winding speed of the vector in the $SU(3)$ subspace (eight-dimensional manifold).

Each Particle is a Specific Allocation Scheme

In this framework, “particles” are no longer fundamental entities but specific budget allocation protocols.

• Electron: It is a vector pattern that allocates budget to $v_{mass}$, $v_{em}$, and $v_{weak}$ but refuses to allocate to $v_{strong}$.

• Neutrino: It is a minimalist, investing budget almost only in $v_{weak}$ (participating only in weak interactions), investing very little in $v_{mass}$, and ignoring everything else.

• Photon: It invests zero in all internal sub-sectors (massless, chargeless, colorless); it dedicates everything to external space $v_{ext}$.

The End of Recursion?

Can this decomposition continue infinitely?

Mathematically, Hilbert space has infinite dimensions, seemingly allowing infinite division. But physically, as we stated in Volume 2, QCA’s discrete structure imposes limits. This recursive decomposition must terminate at some depth—that depth is the number of most fundamental degrees of freedom.

The “ten thousand things” we see are the sum of different choices this ultimate vector makes at this series of cascade branch points. The universe did not create ten thousand different bricks to build the world; the universe merely folded the same clay ($c_{FS}$) into ten thousand different shapes.