Appendix E: Narrow-Band Scattering and FS Distance Derivation

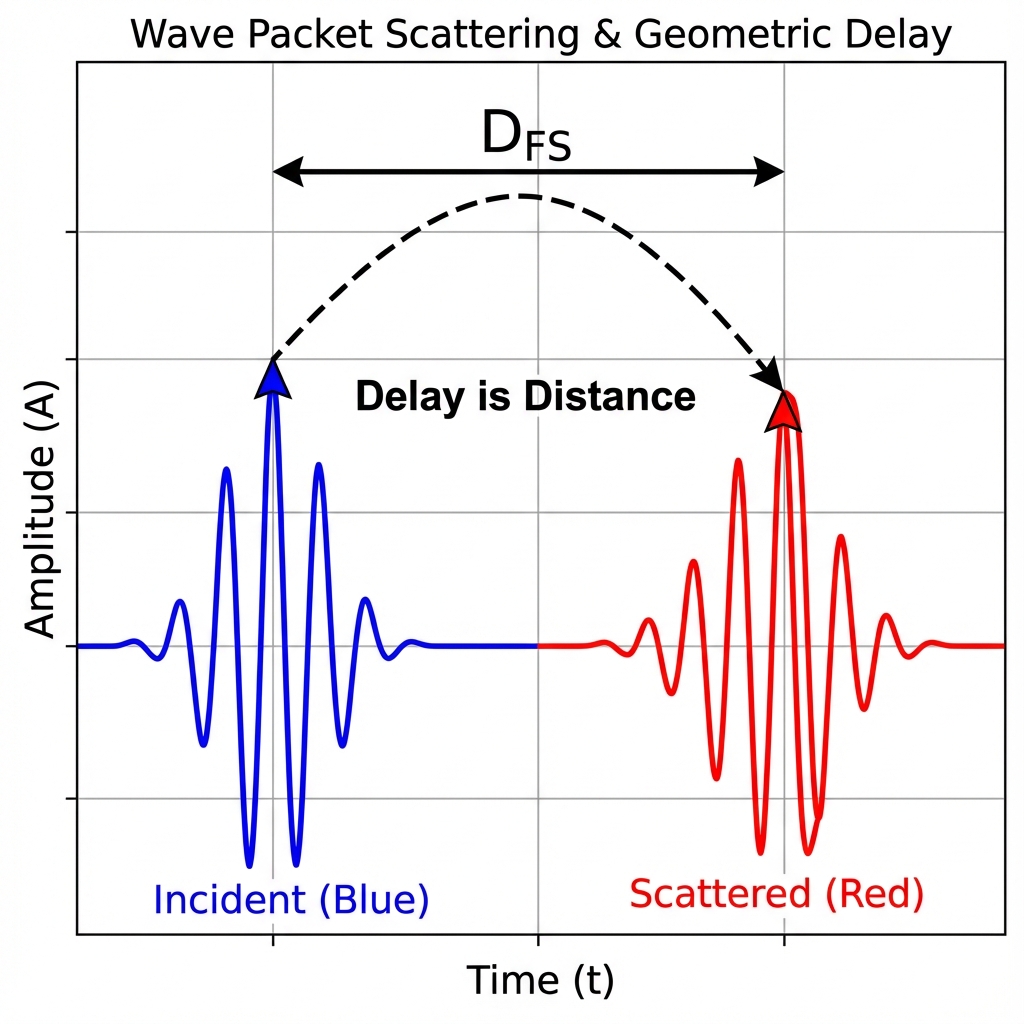
In Chapter 8 “Matter as Topology” of the main text, we proposed a revolutionary geometric perspective: Time Delay in scattering processes is essentially the FS Distance traveled by quantum states in projective Hilbert space. Specifically, for a narrow-band wave packet, a larger delay means it traverses a longer arc length in the internal geometric dimension, resulting in greater geometric distinguishability between the scattered state and the initial state.

This appendix will provide detailed mathematical derivations for this conclusion. We will calculate the overlap integral (visibility) of a Gaussian wave packet after scattering and prove that in the small delay limit, FS distance is strictly proportional to the product of Wigner-Smith time delay and energy bandwidth.

E.1 Scattering Overlap Integral

Consider a single-channel scattering problem with a pure phase scattering matrix $S(\omega )=e^{2i\delta (\omega )}$.

Assume the incident wave packet amplitude $f(\omega )$ is a real Gaussian function centered at ${\omega }_0$ with standard deviation (bandwidth) $\sigma$:

$$|f(\omega ){|}^2=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(\omega -{\omega }_0{)}^2}{2{\sigma }^2}\right)$$

The outgoing state $|{\Psi }_{out}⟩$ is obtained by applying the scattering matrix to the incident state $|{\Psi }_{in}⟩$. To measure the geometric change caused by the scattering process, we need to calculate the Overlap Amplitude between these two states:

$$⟨{\Psi }_{in}|{\Psi }_{out}⟩=\int |f(\omega ){|}^2{e}^{2i\delta (\omega )}d\omega$$

E.2 Phase Linearization and Gaussian Integration

For a Narrow-Band Packet, i.e., when bandwidth $\sigma$ is much smaller than the energy scale where scattering phase changes dramatically, we can expand the phase $\delta (\omega )$ in a Taylor series around the center frequency ${\omega }_0$.

Keeping terms up to first order (linear approximation):

$$\delta (\omega )\approx \delta ({\omega }_0)+{\delta }^{\prime }({\omega }_0)(\omega -{\omega }_0)$$

According to the definition of Wigner-Smith time delay, the derivative of the phase is half the time delay (under the convention $S=e^{2i\delta }$, $T_{WS}={\partial }_{\omega }\delta ({\omega }_0)$ is the single-channel phase half-delay, or typically defined as half the full delay; here we follow the paper’s convention $T_{WS}:={\delta }^{\prime }({\omega }_0)$).

Letting $x=\omega -{\omega }_0$, the integral becomes a standard Gaussian Fourier transform:

$$⟨{\Psi }_{in}|{\Psi }_{out}⟩\approx e^{2i\delta ({\omega }_0)}\int \frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{x^2}{2{\sigma }^2}}{e}^{2i{T}_{WS}x}dx$$

Using the Gaussian integral formula ${\int }_{-\infty }^{\infty }{e}^{-a{x}^2+ikx}dx=\sqrt{\frac{\pi }{a}}{e}^{-k^2/4a}$, where $a=1/(2{\sigma }^2)$ and $k=2T_{WS}$, we can calculate the modulus of the overlap amplitude (i.e., the Visibility V of interference fringes):

$$V:=|⟨{\Psi }_{in}|{\Psi }_{out}⟩|=\exp \left(-2{\sigma }^2{T}_{WS}^2\right)$$

E.3 Geometric Correspondence Between FS Distance and Delay

Now, we convert this physical overlap $V$ to geometric FS distance $D_{FS}$. By definition:

$$V=\cos (D_{FS})$$

In the small delay limit (i.e., $2{\sigma }^2{T}_{WS}^2\ll 1$), we can perform second-order Taylor expansion on both sides:

1. Left side (Gaussian function expansion): $V\approx 1-2{\sigma }^2{T}_{WS}^2$

2. Right side (cosine function expansion): $V\approx 1-\frac{1}{2}{D}_{FS}^2$

Comparing the second-order terms on both sides, we obtain:

$$\frac{1}{2}{D}_{FS}^2\approx 2{\sigma }^2{T}_{WS}^2⟹D_{FS}\approx 2\sigma |T_{WS}|$$

E.4 Physical Conclusions

This derivation rigorously proves the core geometric proposition in the main text:

FS Distance $\approx$ Bandwidth $\times$ Time Delay

This reveals the essence of time delay: it is not a pause on the time axis, but the distance by which the state vector is pulled apart in projective Hilbert space.

• If delay $T_{WS}=0$, then $D_{FS}=0$, and the state undergoes no geometric deflection (except global phase).

• The larger the delay, the more “orthogonal” the outgoing and incoming states become geometrically.

This also provides the mathematical foundation for the “Delay-Fidelity Trade-off”: you cannot simultaneously achieve enormous time delay and maintain perfect quantum state fidelity. Because obtaining delay ($T_{WS}$) itself means you must geometrically move away from the starting point ($D_{FS}$ increases, overlap $V$ decreases). This is an iron law imposed by geometry on signal processing.