1.2 虚数即正交 (Imaginary is Orthogonal)

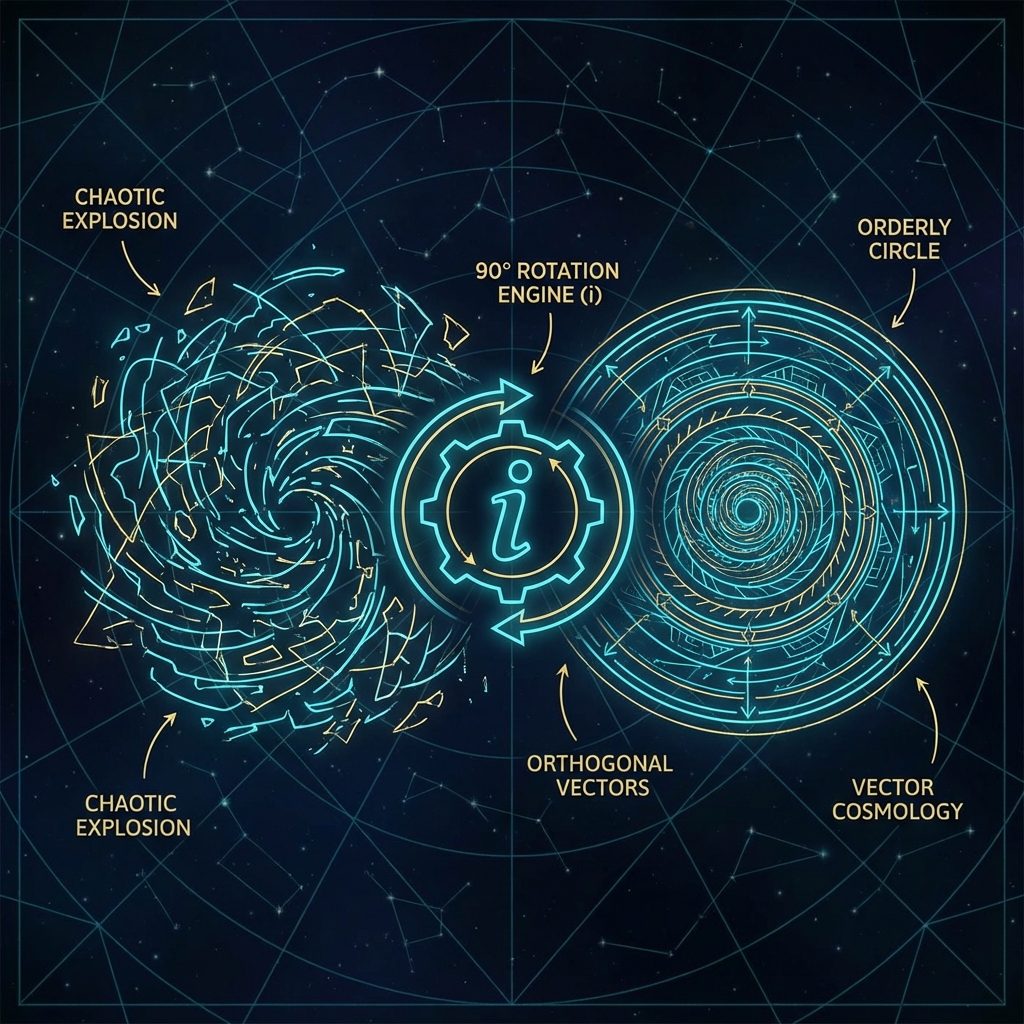
“如果宇宙只是一个指数函数，它早就应该自我毁灭了。那个在指数上不起眼的虚数 $i$，是物理学中最伟大的刹车片。它强行扭转了增长的方向，将一场注定崩溃的爆炸，驯化成了一场永恒优雅的旋转。”

在上一节中，我们赞美了 $e$ 的复利机制。它揭示了宇宙是一个“自驱动“的系统。但是，如果这就是全部真相，那么我们面临一个巨大的麻烦。

纯粹的指数增长 $e^t$ 是极其危险的。

如果哈密顿量 $H$ 仅仅是一个实数，那么薛定谔方程 $|\psi (t)⟩=e^{-Ht}|\psi (0)⟩$ 描述的将不是波动，而是 衰变 或 爆炸。系统的总预算 $c_{FS}$ 会在瞬间耗尽，或者膨胀到无穷大。这样的宇宙无法承载任何稳定的结构。

为了让“存在“得以持续，为了让“圆“能够闭合，宇宙引入了一个神秘的几何修正算符。

这就是 虚数单位 $i$。

在 《矢量宇宙论》 中，$i$ 不是数学家想象出来的幽灵，它是 正交旋转算符 (Orthogonal Rotation Operator)。

90度的魔法

在复平面上，任何数字乘以 $i$，其几何效果都是 逆时针旋转 90 度。

• $1\times i=i$ （转到了虚轴）

• $i\times i=-1$ （转回了实轴，但方向相反）

这个简单的几何操作，当被放入指数函数 $e^{i\theta }$ 中时，产生了数学史上最深刻的震荡：欧拉公式 $e^{i\theta }=\cos \theta +i\sin \theta$。

这告诉我们：带有虚数的指数增长，不再是数量的改变，而是角度的改变。

回到物理学。薛定谔方程中的那个 $-i$，实际上是宇宙底层的一条 “强制转向指令”。

$$|\dot{\psi }⟩=-iH|\psi ⟩$$

这意味着：状态矢量的变化率（$|\dot{\psi }⟩$），必须始终与当前的状态矢量（$|\psi ⟩$）保持垂直（正交）。

• 如果变化率与状态平行（没有 $i$），矢量就会变长或变短（模长改变）。

• 如果变化率与状态垂直（有 $i$），矢量的长度保持不变，只是方向发生偏转。

这就是 幺正性 (Unitarity) 的几何本质。$i$ 是守恒律的守护神。它保证了无论哈密顿量 $H$ 多么巨大，无论演化多么剧烈，全局矢量 $|\Psi ⟩$ 的模长永远锁定为 1。

振动是旋转的投影

这一视角彻底刷新了我们对“波动“的理解。

在经典物理中，我们习惯于“振动“的图像：弹簧的来回伸缩，水波的上下起伏。这是一种线性的、实数的振荡。

但在量子力学中，宇宙不振动，宇宙只旋转。

当我们看到一个粒子表现出正弦波 $\sin (kx-\omega t)$ 的性质时，我们实际上是看到了一个 高维复数螺旋 在实数轴上的投影。

• 那个粒子并没有真的在那儿“抖动“。

• 它的波函数矢量在复数空间中做一个完美的、匀速的圆周运动。

正如我们在第一部书中所述，FS 几何不区分“动“与“静“，只区分“转动“。

所有的能量 $E$，本质上都是 角速度。所有的物理演化，都是 $e^{-iHt}$ 驱动的 相位旋转。

我们之所以觉得世界充满了波动和周期，是因为我们生活在那个旋转矢量的侧面。

守恒与增长的博弈

至此，我们终于看清了 $e$ 和 $i$ 的分工。

• $e$ (指数机制)：提供了 “自驱动” 的动力。它保证了每一刻的演化都基于上一刻的状态，赋予了时间以连续性。

• $i$ (虚数机制)：提供了 “正交性” 的约束。它强迫这种驱动力不做功（不改变模长），只改变方向。

没有 $e$，宇宙是一潭死水。

没有 $i$，宇宙是一场短暂的爆炸。

只有当两者结合，我们才得到了那个 “周行而不殆” 的完美大圆。

在第二部书中，我们讨论了“螺旋“和“维度膨胀“。在那个图景里，虚数 $i$ 的统治似乎出现了一丝松动（或者说，$H$ 获得了一个微小的非厄米虚部），导致旋转变成了对数螺旋 $e^{(\lambda +i\omega )t}$。

但即便是在那样狂野的飞升中，$i$ 所代表的 旋转 依然是主旋律，$\lambda$ 所代表的 增长 只是伴奏。

结论：垂直的真理

所以，虚数并不虚。它是宇宙中最坚硬的几何实体。

它是那堵墙，挡住了无限膨胀的深渊，迫使时间弯曲成环。

当我们理解了 $i$ 的正交本性，我们就理解了为什么量子力学必须是复数的。因为只有在复数空间里，“变化” 才能在不破坏 “存在”（模长守恒）的前提下发生。

现在，我们已经掌握了演化的引擎（$e$）和方向盘（$i$）。接下来的问题是：这个引擎驱动着矢量去往何方？

既然宇宙不选择单一的道路，既然波函数弥散在整个空间，那么这无数条可能的轨迹是如何汇聚成我们所看到的唯一历史的？

这引出了下一章的主题：路径积分。我们将看到，$e$ 的指数不仅描述了单一的旋转，它还描述了所有可能历史的 总和。