Appendix C: Lie Algebras and the Exponential Map

In Volume II “The Generator” of Vector Cosmology III, we described the Hamiltonian $H$ as the “seed” of cosmic evolution, and $e$ as the “machine” that unfolds this seed into the long river of time. The mathematical structure behind this physical picture is one of the most magnificent edifices in modern mathematics—Lie Groups and Lie Algebras.

This appendix provides a rigorous mathematical description of this structure. We will prove why any continuous symmetry (such as time translation, space rotation) must necessarily be generated by an infinitesimal “tangent vector” (generator) through the exponential map $e^X$. This is mathematical proof that “the derivative is the ontology.”

C.1 Curved Groups and Flat Algebras

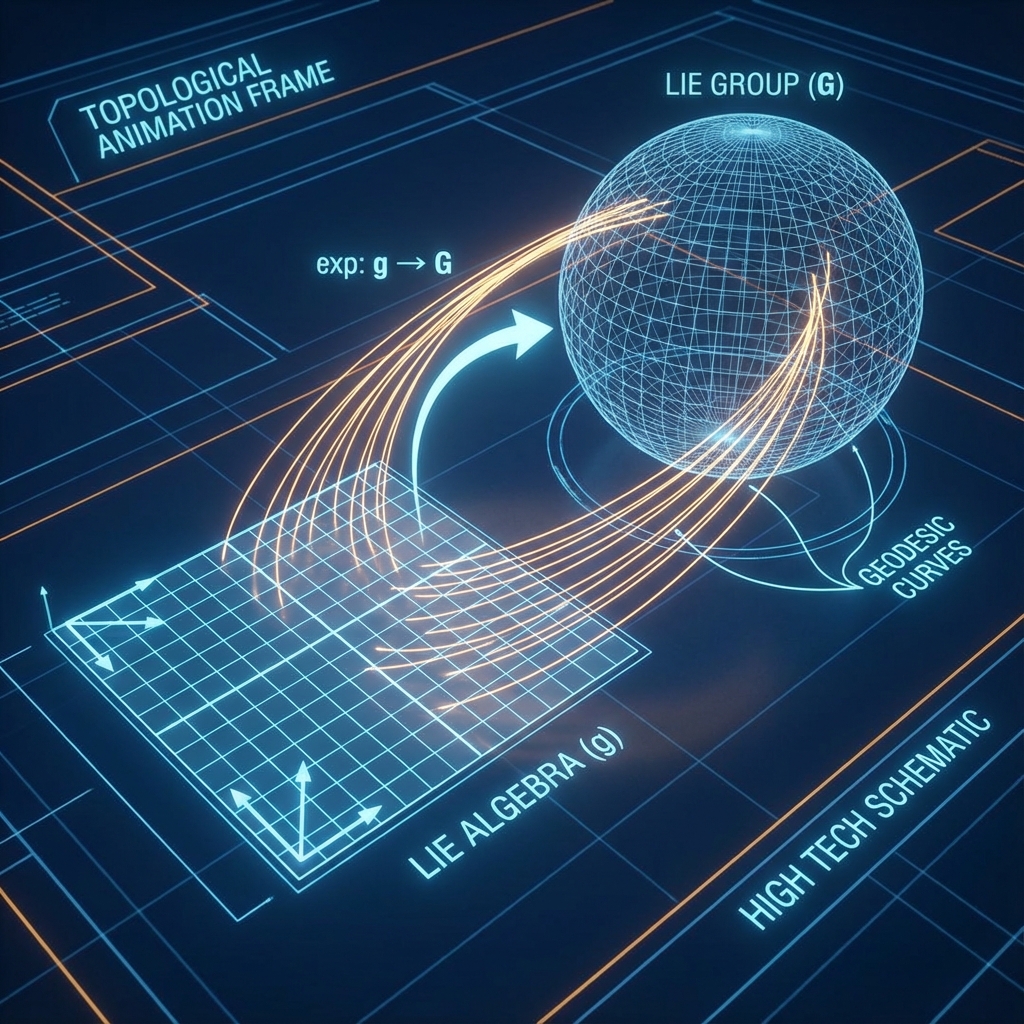
Symmetry operations in physics typically form a Lie Group ($G$). For example, all possible spatial rotations form the $SO(3)$ group, and all time translations form the $T(1)$ group (isomorphic to the real axis $\mathbb{R}$). A Lie group is a smooth manifold—it is both a group (can operate) and a space (can differentiate).

However, Lie groups are usually curved and nonlinear (like the Earth’s surface). Direct study is difficult.

To simplify the problem, mathematician Sophus Lie discovered a brilliant method: study only the Tangent Space at the identity element $e$ (Identity, i.e., “no operation”) of the group.

This tangent space is called the Lie Algebra ($\mathfrak{g}$).

• $\mathfrak{g}$ is linear: It is a vector space. You can add generators and multiply by scalars.

• $\mathfrak{g}$ is infinitesimal: It represents the trend of group elements at the instant they “just begin to change.”

C.2 Exponential Map: The Bridge Connecting Two Worlds

How do we return from the infinitesimal tangent space $\mathfrak{g}$ to the grand group manifold $G$?

This requires the Exponential Map:

$$\exp :\mathfrak{g}\to G$$

For matrix Lie groups (most cases in physics), this map is the matrix exponential we learned in advanced algebra:

$$e^X=\sum _{k=0}^{\infty }\frac{X^k}{k!}=I+X+\frac{1}{2}{X}^2+\dots$$

Theorem: For any element $X\in \mathfrak{g}$ in the Lie algebra, $e^{tX}$ (where $t\in \mathbb{R}$) forms a One-Parameter Subgroup in the Lie group $G$.

$$g(t)=e^{tX}$$

satisfying $g(t+s)=g(t)g(s)$.

Physical meaning:

• $X$ (Generator): Not just a tangent vector, it is the “initial velocity” of a Geodesic.

• $e^{tX}$ (Orbit): The complete trajectory “gliding” on the manifold from this initial velocity.

The universe need not remember the entire trajectory; the universe only needs to remember the starting point and initial velocity $X$ (i.e., the Hamiltonian).

C.3 Hamiltonian as Tangent Vector

In quantum mechanics, the unitary evolution group $U(t)$ is a Lie group ($U(N)$ or infinite-dimensional unitary group).

Schrödinger’s equation defines its tangent vector:

$$\frac{d}{dt}U(t){|}_{t=0}=-iH$$

Here $-iH$ is the Lie algebra element.

• Because $U$ is unitary ($U^{†}U=I$), $-iH$ must be Anti-Hermitian.

• This means $H$ must be Hermitian (requirement for physical observables).

So, what physicists call the “energy operator $H$” is, in the geometer’s eyes, a tangent vector in the tangent space at the identity of the unitary group.

It defines the “direction” of cosmic evolution.

C.4 Why Must It Be $e$?

Why must the evolution operator be $e^{-iHt}$? Why not $2^{-iHt}$ or $\sin (Ht)$?

This is a uniqueness theorem about Homomorphisms.

We require time evolution to satisfy two basic conditions:

1. Continuity: $U(t)$ changes smoothly with $t$.

2. Semigroup property: $U(t_1+t_2)=U(t_1)U(t_2)$ (evolving $t_1$ then $t_2$ equals directly evolving $t_1+t_2$).

Mathematical theorem states: The only non-trivial continuous function form satisfying the above conditions is the exponential function.

This fundamentally explains why nature chose $e$.

$e$ is not an arbitrary constant; $e$ is the mathematical form logically necessitated by “continuity” and “causal accumulation”. As long as we admit that time flows continuously and past history accumulates to the present, the universe must drive itself through $e$.