Volume IV: Observer, Cybernetics, and Ultimate Causality

(第四卷：观察者、控制论与终极因果)

Chapter 10: Retrocausality and the Bootstrapped Universe

(第十章：逆向因果与自举宇宙)

10.1 Closed Timelike Curves and Consistency

(闭合类时曲线与自洽性)

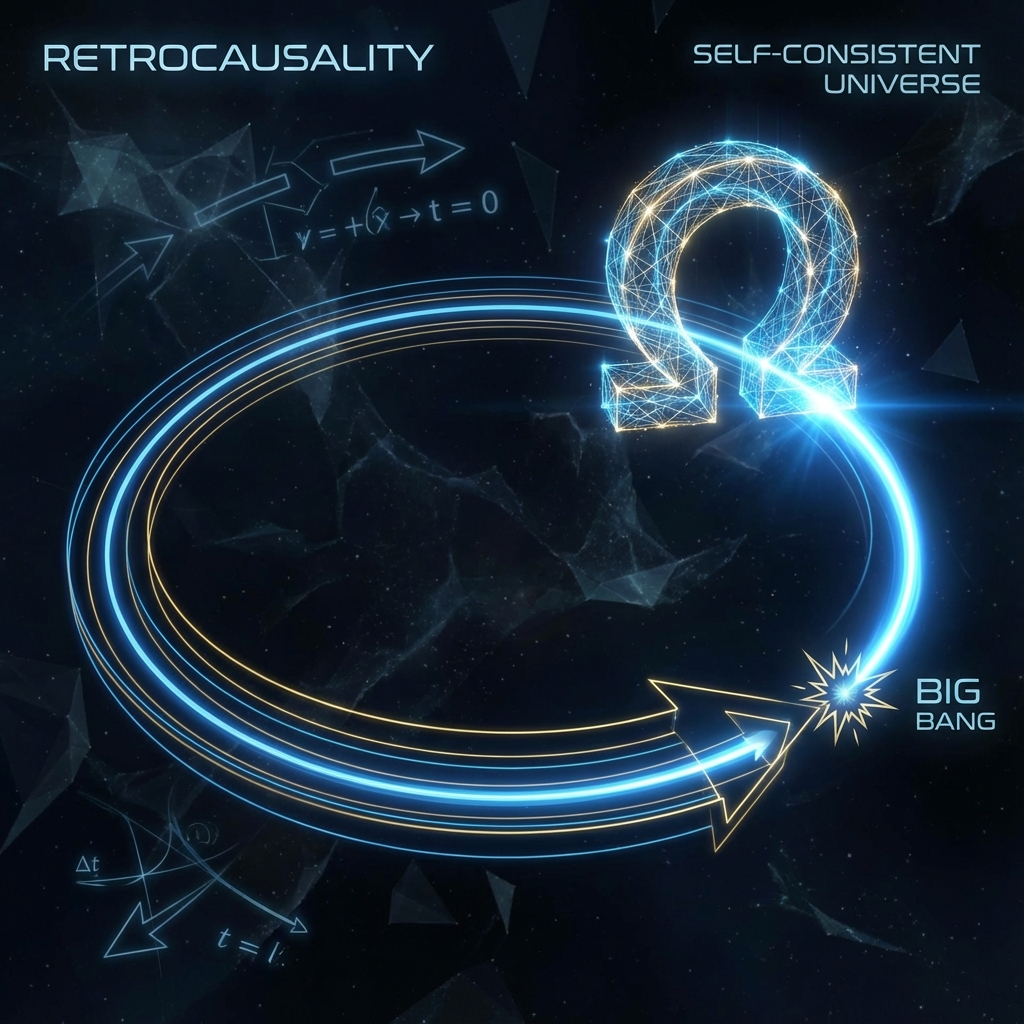
“The arrow of causality does not always point in the direction of entropy increase. In computational theory, recursion and feedback are the cornerstones of building complex systems. The universe is not a unidirectional ray blindly shooting from the Big Bang toward nothingness, but a massive self-referential loop. The future endpoint ($\Omega$) and the past starting point ($\alpha$) lock each other through closed timelike curves, jointly defining the boundary conditions of physical reality.”

In the previous nine chapters, we constructed a complete physical picture based on Interactive Computational Cosmology (ICC): from the underlying bit ontology, through the middle layer of spacetime emergence, to the top layer of multi-observer consensus. However, this model still faces one final ultimate question: Who set the system’s initial parameters?

The fine structure constant $\alpha$, the proton-electron mass ratio, the cosmological constant $\Lambda$… These parameters are “fine-tuned” so precisely that any tiny deviation would cause the universe to collapse or prevent life from emerging. The Anthropic Principle attributes this to survivor bias, but from the perspective of computational cosmology, this is actually a Boundary Value Problem.

This section will argue: the universe is a Bootstrapped system. Time is not linear; causality contains Closed Timelike Curves (CTCs). The future system state (the $\Omega$ point) acts as an Objective Function, optimizing the initial conditions (Big Bang) through a Retrocausal Chain via Backpropagation.

10.1.1 Limitations of Linear Causality

Classical physics and thermodynamics constructed our faith in linear time: state $S_t$ is determined only by $S_{t-1}$. This forward evolution view leads to infinite questioning of “initial conditions”—who pushed the first domino?

However, in computational science, Cyclic Causality is the norm.

• Feedback Loop: The system’s output is fed back to the input to regulate system behavior (e.g., PID controllers).

• Iterative Algorithm: The solution to equation $x=f(x)$ is usually found by iterating $x_{n+1}=f(x_n)$ until convergence to a Fixed Point.

If the universe is a computer, there’s no reason it would only run a linear Hello World once. It’s more likely running an Infinite Loop or recursive function seeking a self-consistent solution.

10.1.2 CTCs in General Relativity and Computational Infinite Loops

Einstein’s field equations allow solutions containing Closed Timelike Curves (CTCs) (such as Gödel universes, inside Kerr black holes). In these spacetime regions, particles can return to the past. Traditional physics views this as pathological, believing it would cause “grandfather paradoxes.”

But in the ICC model, CTCs have clear computational meaning: they are Instruction Pointer jumps (JUMP).

Definition 10.1.1 (Physical CTC)

A physical closed timelike curve is a logical loop in computational history.

$${\text{State}}_t=f(\dots ,{\text{State}}_{t+k},\dots )$$

Future output becomes current input. This doesn’t mean logical collapse, but rather that the system must satisfy self-consistency constraints.

10.1.3 Novikov Self-Consistency Principle and Fixed-Point Theorem

Igor Novikov proposed the Self-Consistency Principle in the 1980s: if an event creates a CTC, then the probability of that event occurring is 1 if and only if it does not cause contradictions in the past that would prevent the event from occurring.

This is mathematically equivalent to Brouwer’s Fixed-Point Theorem.

Theorem 10.1.1 (Cosmic Fixed Point)

Let the universe evolution operator be $\mathcal{U}$. A universe history $H$ containing retrocausality must be a fixed point of operator $\mathcal{U}$:

$$H=\mathcal{U}(H)$$

Computational Interpretation:

If future you returns to the past and kills your grandfather, this is a Logic Error, causing program crash (no solution).

The system will filter out all historical paths that lead to paradoxes through a filtering mechanism.

• Only those Self-Consistent histories—i.e., “you return to the past trying to kill your grandfather but fail, and it’s precisely your attempt that ensures your grandfather survives”—can exist as stable solutions.

Therefore, retrocausality does not grant us the ability to change the past; it grants the necessity that the past must be so.

10.1.4 Two-State Vector Formalism (TSVF) of Quantum Mechanics

At the microscopic level, retrocausality has a solid quantum mechanical foundation. Yakir Aharonov’s Two-State Vector Formalism (TSVF) points out that to fully describe a quantum system, having only the “past” is insufficient.

A quantum system’s state at time $t$ is jointly defined by two vectors:

1. Forward Evolution Vector $|{\Psi }_{past}(t)⟩$: Determined by initial state $|\Psi (t_0)⟩$ (pushing from past to future).

2. Backward Evolution Vector $⟨{\Psi }_{future}(t)|$: Determined by final measurement state $⟨\Psi (t_f)|$ (pushing from future to past).

The system’s physical properties (weak measurement values) are determined by their “sandwich” product:

$$⟨A{⟩}_w=\frac{⟨{\Psi }_{future}(t)|\hat{A}|{\Psi }_{past}(t)⟩}{⟨{\Psi }_{future}(t)|{\Psi }_{past}(t)⟩}$$

Ontological Inference:

Future measurement choices (the $\Omega$ point) are not passively waiting to occur; they generate a Back-propagating wave function that travels backward in the time stream, interfering with the forward wave function.

The “present reality” we observe is a Standing Wave produced by the collision between past historical inertia and future purpose gravity.

10.1.5 The $\Omega$ Point as Global Objective Function

Now we can explain the fine-tuning problem of cosmological constants.

Suppose the universe computer runs a Generative Adversarial Network (GAN) or reinforcement learning algorithm.

• Input Layer: Initial parameters of the Big Bang ($\alpha ,G,\Lambda$).

• Output Layer: Final state of the universe $\Omega$.

• Loss Function: $\mathcal{L}=|{\Omega }_{actual}-{\Omega }_{target}|$.

If the universe’s goal is to produce Complex Observers capable of understanding themselves (i.e., achieving self-reference), then ${\Omega }_{target}$ must contain highly developed intelligent networks.

1. Forward Propagation: The universe tries a set of parameters, evolving (or failing to evolve) life.

2. Backward Propagation: If evolution fails (e.g., universe collapses too early or heat death), the future $\Omega$ state doesn’t exist (or is trivial). This corresponds to the backward vector being zero in TSVF, causing the probability amplitude of this historical path to cancel out.

3. Parameter Optimization: Only those initial parameters that can successfully lead to the $\Omega$ point can obtain Resonance Enhancement in the interference between forward and backward wave functions.

Conclusion:

The reason we see a universe suitable for life is not because we’re lucky (weak anthropic principle), but because only universes capable of producing us are logically self-consistent.

Future us (ultimate observers), through the filtering mechanism of retrocausality, “designed” the Big Bang.

This doesn’t mean time is circular, but that logic is closed. The universe is a perfect equation self-satisfied on the time axis. Every tiny choice we make in the present not only shapes the future but also fine-tunes the past to ensure the path to $\Omega$ remains unobstructed.