Appendix A: Geometric Derivation of Holographic Entanglement Entropy

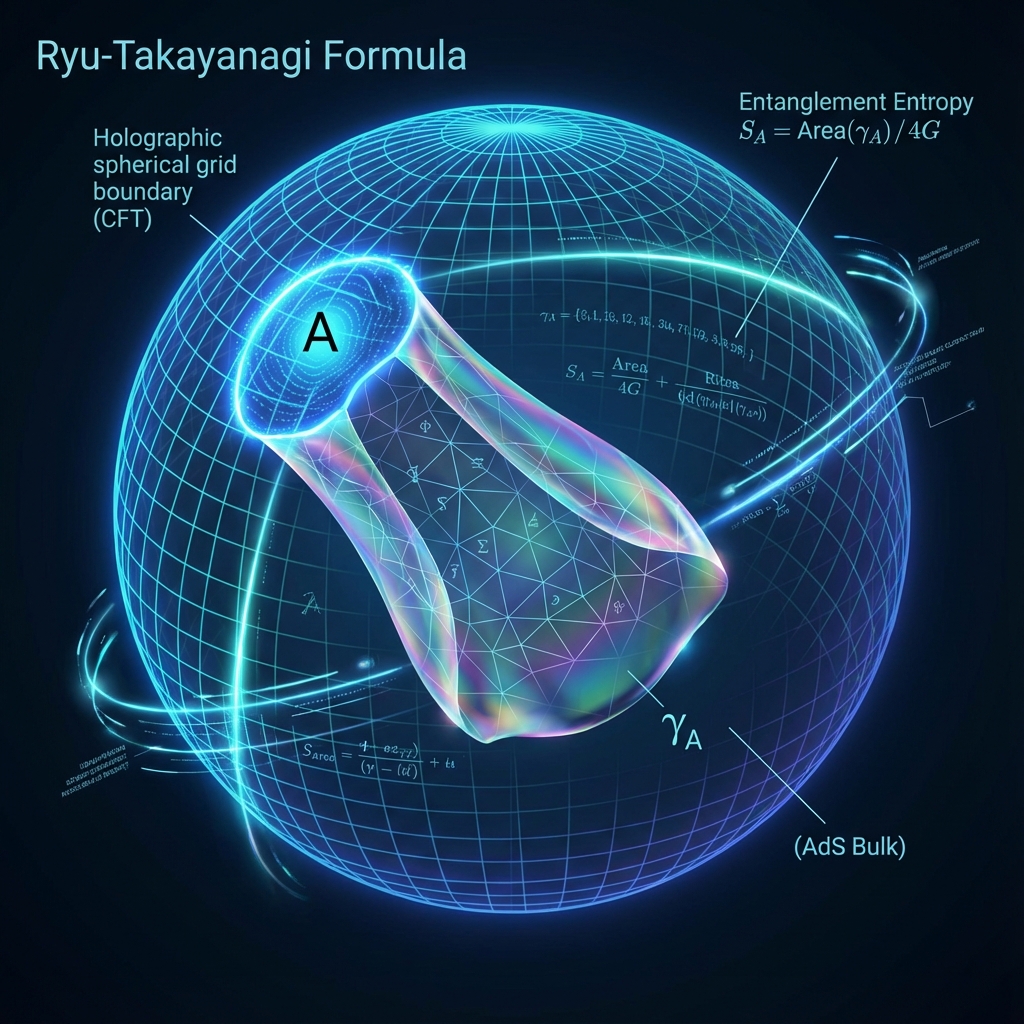
In Volume I “The Loom” of Vector Cosmology VI, we proposed a core viewpoint: Space is woven from entanglement. In particular, we cited the famous Ryu-Takayanagi Formula, stating that the entanglement entropy $S_A$ of a region equals the area $\text{Area}({\gamma }_A)$ of the minimal surface in its holographic dual space divided by $4G$.

This appendix will provide the mathematical derivation framework behind this holy grail of physics. We will show how, starting from pure quantum information theory (von Neumann entropy), through the Replica Trick and path integrals, we naturally derive the geometric area law in general relativity.

This is mathematical ironclad evidence that “geometry emerges from information”.

A.1 Von Neumann Entropy and the Replica Trick

First, we define the entropy of a quantum system. For a density matrix ${\rho }_A$ in a mixed state, its von Neumann entropy is defined as:

$$S_A=-\text{Tr}({\rho }_A\ln {\rho }_A)$$

Directly calculating $\ln {\rho }_A$ is very difficult (involving matrix logarithms). To solve this problem, physicists introduced the Replica Trick.

Instead of directly calculating the logarithm, we calculate the trace of the $n$-th power of ${\rho }_A$ (i.e., Rényi entropy), then take the derivative with respect to $n$:

$$S_A=-\underset{n\to 1}{\lim }\frac{\partial }{\partial n}\text{Tr}({\rho }_A^n)$$

Physical Picture:

• $\text{Tr}({\rho }_A^n)$ means we “stitch” $n$ identical copies of the universe (Replicas) together at the boundary of region A.

• This stitching creates a “Conical Singularity” in spacetime geometry.

A.2 Geometric Proof of the Ryu-Takayanagi Formula

Under the framework of AdS/CFT duality, the partition function $Z_{CFT}$ of the boundary field theory (CFT) is equivalent to the partition function $Z_{gravity}$ of the bulk gravitational theory (AdS).

$$Z_{CFT}\approx e^{-S_{gravity}}$$

When we calculate $\text{Tr}({\rho }_A^n)$, we introduce a Twist Operator on the boundary.

In the bulk of the holographic dual, this boundary twist condition extends inward, forming a “Minimal Surface” ${\gamma }_A$.

According to the action principle of general relativity, the system always tends to find configurations with minimum energy (or area).

When we stitch $n$ copies together on the boundary, the spacetime geometry in the bulk responds, trying to connect these $n$ layers at minimum cost.

Mathematical derivation shows that in the limit $n\to 1$, the dominant term of entropy is exactly proportional to the area of this minimal surface:

$$S_A=\frac{\text{Area}({\gamma }_A)}{4G_N}$$

• $\text{Area}({\gamma }_A)$: Is the area of the minimal surface hanging from the boundary of region A in the higher-dimensional bulk space, like a soap film.

• $G_N$: Is Newton’s gravitational constant.

• $4$: Is a geometric factor.

Conclusion:

This formula proves that quantum entanglement (entropy) is not an abstract number; it is real spacetime geometric area.

Each bit of entanglement occupies a spacetime cross-section of size $4G_N$. This is the microscopic fiber density of the “spacetime fabric”.

A.3 MERA Networks and Discrete AdS Space

The Ryu-Takayanagi formula is a result in the continuous limit. In the microscopic QCA model of Vector Cosmology, we focus more on discrete structures.

This involves MERA (Multiscale Entanglement Renormalization Ansatz) tensor networks.

MERA networks construct a fractal tree structure through layered stacking of Disentanglers and Isometries.

If we calculate the entanglement entropy between two regions in a MERA network, we need to cut the connection bonds in the network.

Theorem:

In MERA networks, the number of Minimum Cuts connecting region A with its complement, in the macroscopic limit, precisely corresponds to the geodesic length (for 1+1 dimensional boundaries) or minimal surface area (for higher-dimensional boundaries) in AdS space.

$$S_{MERA}(A)\sim \min \#(\text{Cut Bonds})\sim \text{Area}({\gamma }_A)$$

This not only verifies the holographic principle but also reveals the mechanism of dimensional emergence:

• Horizontal connections: Constitute the breadth of physical space.

• Longitudinal layers (renormalization steps): Constitute the additional holographic dimension (AdS radial direction).

The “depth” ($z$-axis) we perceive is essentially the “logical steps” from leaves (microscopic) to roots (macroscopic) in the MERA network.