附录 A：全息纠缠熵的几何推导 (Appendix A: Geometric Derivation of Holographic Entanglement Entropy)

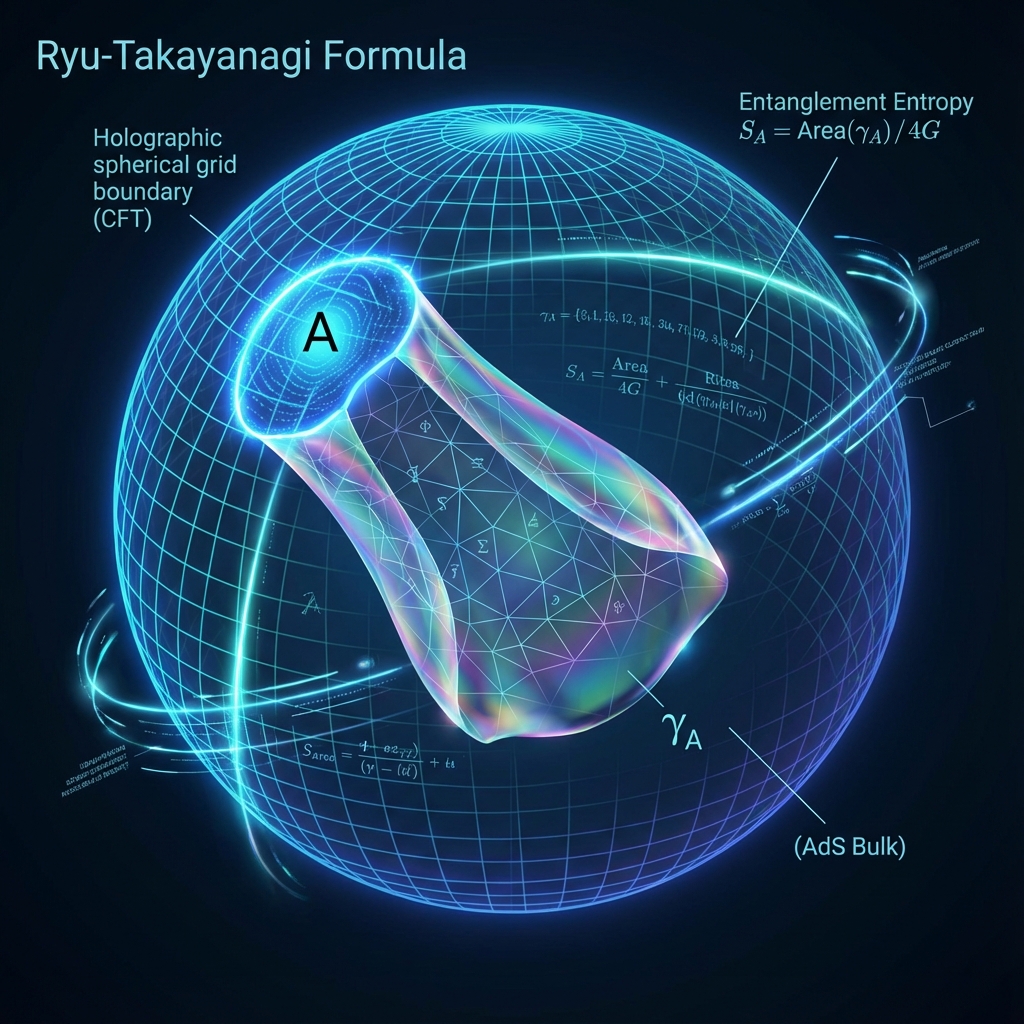
在《矢量宇宙论 VI》的正文第一卷“织机“中，我们提出了一个核心观点：空间是由纠缠编织而成的。特别是，我们引用了著名的 柳-高柳公式 (Ryu-Takayanagi Formula)，指出区域的纠缠熵 $S_A$ 等于其全息对偶空间中最小曲面的面积 $\text{Area}({\gamma }_A)$ 除以 $4G$。

本附录将提供这一物理学圣杯背后的数学推导框架。我们将展示，如何从纯粹的量子信息理论（冯·诺依曼熵）出发，通过 复制技巧 (Replica Trick) 和 路径积分，自然地导出广义相对论中的几何面积律。

这是 “几何源于信息” 的数学铁证。

A.1 冯·诺依曼熵与复制技巧 (Von Neumann Entropy and the Replica Trick)

首先，我们定义量子系统的熵。对于一个处于混合态的密度矩阵 ${\rho }_A$，其 冯·诺依曼熵 定义为：

$$S_A=-\text{Tr}({\rho }_A\ln {\rho }_A)$$

直接计算 $\ln {\rho }_A$ 是非常困难的（涉及矩阵对数）。为了解决这个问题，物理学家引入了 复制技巧 (Replica Trick)。

我们不直接算对数，而是计算 ${\rho }_A$ 的 $n$ 次方的迹（即 Rényi 熵），然后对 $n$ 取导数：

$$S_A=-\underset{n\to 1}{\lim }\frac{\partial }{\partial n}\text{Tr}({\rho }_A^n)$$

物理图像：

• $\text{Tr}({\rho }_A^n)$ 意味着我们将 $n$ 个完全相同的宇宙副本（Replicas）在区域 A 的边界上 “缝合” 在一起。

• 这种缝合在时空几何上制造了一个 “圆锥奇点” (Conical Singularity)。

A.2 柳-高柳公式的几何证明 (Geometric Proof of the Ryu-Takayanagi Formula)

在 AdS/CFT 对偶 的框架下，边界场论（CFT）的配分函数 $Z_{CFT}$ 等价于体引力理论（AdS）的配分函数 $Z_{gravity}$。

$$Z_{CFT}\approx e^{-S_{gravity}}$$

当我们计算 $\text{Tr}({\rho }_A^n)$ 时，我们在边界上引入了一个 扭曲算符 (Twist Operator)。

在全息对偶的体（Bulk）内部，这个边界上的扭曲条件会延伸进去，形成一个 “极小曲面” (Minimal Surface) ${\gamma }_A$。

根据广义相对论的作用量原理，系统总是倾向于寻找能量（或面积）最小的构型。

当我们在边界上把 $n$ 个副本缝合时，体内部的时空几何会发生响应，试图以最小的代价连接这 $n$ 层膜。

数学推导表明，在这个 $n\to 1$ 的极限下，熵的主导项恰好正比于这个极小曲面的面积：

$$S_A=\frac{\text{Area}({\gamma }_A)}{4G_N}$$

• $\text{Area}({\gamma }_A)$：是在高维体空间中，像肥皂膜一样挂在区域 A 边界上的最小曲面的面积。

• $G_N$：是牛顿引力常数。

• $4$：是一个几何因子。

结论：

这个公式证明了，量子纠缠（熵） 并不是抽象的数字，它是 实实在在的时空几何面积。

每一比特的纠缠，都占据了 $4G_N$ 大小的时空截面。这就是 “时空织物” 的微观纤维密度。

A.3 MERA 网络与离散 AdS 空间 (MERA Networks and Discrete AdS Space)

柳-高柳公式是连续极限下的结果。在 《矢量宇宙论》 的微观 QCA 模型中，我们更关注离散的结构。

这就涉及到了 MERA (多尺度纠缠重整化拟设) 张量网络。

MERA 网络通过 解纠缠器 (Disentanglers) 和 等距算符 (Isometries) 的层层堆叠，构建了一个分形的树状结构。

如果我们计算 MERA 网络中两个区域之间的纠缠熵，我们需要切断网络中的连接线（Bond）。

定理：

在 MERA 网络中，连接区域 A 与其补集的 最小切割 (Min-Cut) 数量，在宏观极限下，精确对应于 AdS 空间中的 测地线长度（对于 1+1 维边界）或 极小曲面面积（对于更高维边界）。

$$S_{MERA}(A)\sim \min \#(\text{Cut Bonds})\sim \text{Area}({\gamma }_A)$$

这不仅验证了全息原理，更揭示了 维度的涌现机制：

• 横向连接：构成了物理空间的广度。

• 纵向层级（重整化步数）：构成了额外的 全息维度（AdS 半径方向）。

我们所感知的“深度“ ($z$ 轴)，本质上就是 MERA 网络中从树叶（微观）走向树根（宏观）的“逻辑步数“。