The Omega Framework

8.3 负时间的解毒剂 (The Antidote to Negative Time)

“In the logic of geometry, there is no regret medicine, nor time machines. The so-called ‘time reversal’ is merely a dangerous phase gymnastics that the wave function performs in projective space to take shortcuts.”

在量子散射理论的深处，隐藏着一个幽灵般的悖论，长期以来困扰着物理学家的直觉。这就是 负 Wigner-Smith 时间延迟 (Negative Time Delay)。

根据公式，时间延迟对应于散射相位对能量的导数 ($\tau \sim \partial \varphi /\partial \omega$)。在某些特殊的物理情境下（例如光线经过特定的介质或粒子经过特定的势垒），这个导数可以是负的。这意味着，粒子似乎在“进入“散射区域之前就已经“出来“了。

这听起来像是违背因果律的魔法，甚至暗示了时光倒流的可能性。但在 《矢量宇宙论》 的几何审视下，这个悖论瞬间瓦解。我们不需要引入逆向的时间，我们只需要理解 相位的几何学。

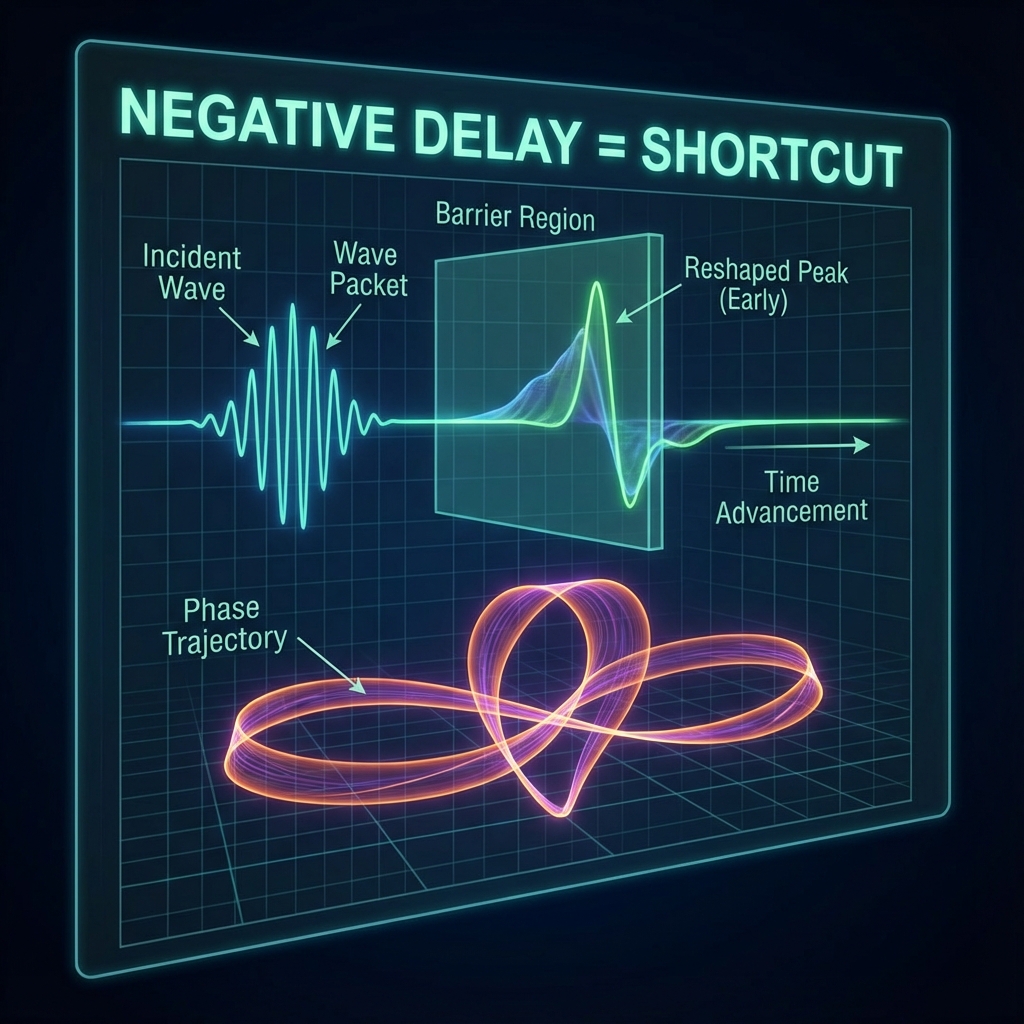
8.3.1 并不存在的倒流：重塑而非穿越

首先，我们必须确立一个绝对的公理：宇宙的矢量永远向前旋转。

在我们的微观 QCA 架构中，全局状态 $|\Psi (\tau )⟩$ 随内禀时间 $\tau$ 的演化是由幺正算符 $U$ 驱动的。这个过程是严格单调的，没有任何机制允许 $\tau$ 倒流。

那么，负延迟是怎么发生的？

它不是时间的倒流，它是 波包的重塑 (Reshaping)。

想象一个很长的列车（波包）进入隧道。

• 正常情况（正延迟）：列车在隧道里减速，车头晚点到达出口。

• 负延迟情况：隧道里的机制（干涉）切断了列车的尾巴，并将能量重新堆积到了车头。结果是，虽然列车的“重心“或“峰值“比预期的早到了，但列车的 车头（前沿） 并没有超越光速，也没有超越它原本应该到达的极限位置。

在 FS 几何中，负延迟意味着散射态矢量在射影空间中采取了一条特殊的路径，使得出射波包的峰值相位呈现出“提前量“。但这是一种干涉效应，而非违反因果律的实体移动。

8.3.2 相位的回溯：捷径的代价

既然没有违背因果律，那么这种“提前“是免费的吗？

不。在 《矢量宇宙论》 的经济学中，没有任何东西是免费的。为了制造“负时间“的幻觉，系统必须支付昂贵的 几何代价。

让我们回到 FS-莱文森关系。对于标准的散射过程（如共振），相位 $\varphi (\omega )$ 是单调增加的，此时 FS 轨迹的长度 $L_{FS}$ 恰好等于拓扑缠绕数 $N_b\pi$。这是“最省钱“的路径。

但是，当出现负时间延迟时，意味着相位 $\varphi (\omega )$ 在局部发生了 回溯 (Backtracking)——它不仅没有增加，反而暂时减少了。

这种回溯在几何上意味着什么？

这意味着矢量在射影希尔伯特空间中并没有顺滑地绕圈，而是进行了一次复杂的“折返跑“。为了让相位导数变负，矢量必须在多余的维度上划过更长的弧线。

结论是惊人的：

凡是表现出负时间延迟的过程，其 FS 几何路径长度 $L_{FS}$ 必然严格大于拓扑下界 $N_b\pi$。

你以为你通过负延迟“节省“了时间？不，你在几何上 跑了更远的路。你支付了额外的 $c_{FS}$ 预算来构建那个复杂的干涉结构，从而在宏观上伪造了一个“提前到达“的假象。

8.3.3 因果律的铁壁：QCA 的保证

最终，微观引擎保证了这一切不会失控。

无论波包如何重塑，无论相位如何回溯，底层的 量子元胞自动机 (QCA) 始终受到 Lieb-Robinson 速度 ($v_{LR}$) 的限制。

• 宏观上的“群速度“或“Wigner-Smith 延迟“只是波包峰值的统计行为，它们在数学上可以超光速甚至为负。

• 但微观上的 信息传播速度（信号的前沿）绝不可能超过 $c_{FS}$（即 $v_{LR}$）。

因此，负时间延迟是一个 “几何解毒剂”：它解除了我们对因果律的担忧。它告诉我们，所谓的“快于光“或“早于因“，只是波函数在内部几何维度上玩弄的一种相消干涉的把戏。

宇宙没有时间机器。 那个唯一的矢量始终在不可逆转地绘制着大圆。那些看似逆流的浪花，不过是深水中更为剧烈的湍流在表面的投影。