附录 E：窄带散射与 FS 距离推导 (Appendix E: Narrow-Band Scattering and FS Distance Derivation)

在正文的第 8 章“物质即拓扑“中，我们提出了一个颠覆性的几何观点：散射过程中的 时间延迟 (Time Delay) 本质上是量子态在射影希尔伯特空间中走过的 FS 距离 (FS Distance)。具体而言，对于一个窄带波包，其延迟越大，意味着它在内部几何维度上划过的弧长越长，从而导致散射后的状态与初始状态在几何上的区分度越大。

本附录将对这一结论提供详细的数学推导。我们将计算一个高斯波包经过散射后的重叠积分（可见度），并证明在小延迟极限下，FS 距离严格正比于 Wigner-Smith 时间延迟与能量带宽的乘积。

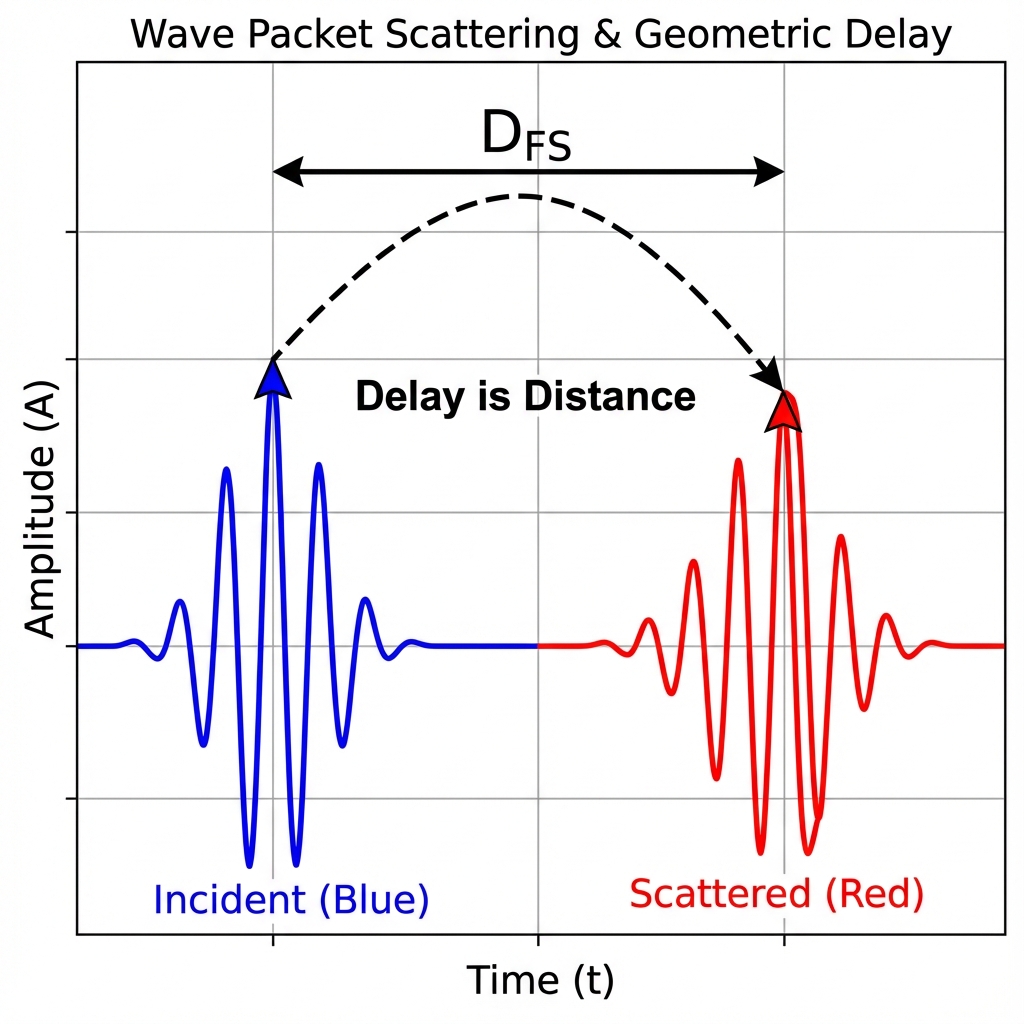
E.1 散射重叠积分

考虑一个单通道散射问题，其散射矩阵为纯相位形式 $S(\omega )=e^{2i\delta (\omega )}$。

假设入射波包的幅度 $f(\omega )$ 是一个中心在 ${\omega }_0$、标准差（带宽）为 $\sigma$ 的实高斯函数：

$$|f(\omega ){|}^2=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(\omega -{\omega }_0{)}^2}{2{\sigma }^2}\right)$$

出射态 $|{\Psi }_{out}⟩$ 由散射矩阵作用于入射态 $|{\Psi }_{in}⟩$ 得到。为了衡量散射过程造成的几何改变，我们需要计算这两个态之间的 重叠幅度 (Overlap Amplitude)：

$$⟨{\Psi }_{in}|{\Psi }_{out}⟩=\int |f(\omega ){|}^2{e}^{2i\delta (\omega )}d\omega$$

E.2 相位线性化与高斯积分

对于 窄带波包 (Narrow-Band Packet)，即带宽 $\sigma$ 远小于散射相位发生剧烈变化的能量尺度，我们可以将相位 $\delta (\omega )$ 在中心频率 ${\omega }_0$ 附近进行泰勒展开。

保留到一阶项（线性近似）：

$$\delta (\omega )\approx \delta ({\omega }_0)+{\delta }^{\prime }({\omega }_0)(\omega -{\omega }_0)$$

根据 Wigner-Smith 时间延迟的定义，相位的导数即为时间延迟的一半（在 $S=e^{2i\delta }$ 的约定下，$T_{WS}={\partial }_{\omega }\delta ({\omega }_0)$ 为单通道相位半延迟，或通常定义为全延迟的一半，此处沿用论文约定 $T_{WS}:={\delta }^{\prime }({\omega }_0)$）。

令 $x=\omega -{\omega }_0$，积分变为标准的高斯傅里叶变换形式：

$$⟨{\Psi }_{in}|{\Psi }_{out}⟩\approx e^{2i\delta ({\omega }_0)}\int \frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{x^2}{2{\sigma }^2}}{e}^{2i{T}_{WS}x}dx$$

利用高斯积分公式 ${\int }_{-\infty }^{\infty }{e}^{-a{x}^2+ikx}dx=\sqrt{\frac{\pi }{a}}{e}^{-k^2/4a}$，其中 $a=1/(2{\sigma }^2)$，$k=2T_{WS}$，我们可以算出重叠幅度的模长（即干涉条纹的 可见度 V）：

$$V:=|⟨{\Psi }_{in}|{\Psi }_{out}⟩|=\exp \left(-2{\sigma }^2{T}_{WS}^2\right)$$

E.3 FS 距离与延迟的几何对应

现在，我们将这个物理上的重叠度 $V$ 转换为几何上的 FS 距离 $D_{FS}$。根据定义：

$$V=\cos (D_{FS})$$

在小延迟极限下（即 $2{\sigma }^2{T}_{WS}^2\ll 1$），我们可以对等式两边进行二阶泰勒展开：

1. 左边（高斯函数展开）：$V\approx 1-2{\sigma }^2{T}_{WS}^2$

2. 右边（余弦函数展开）：$V\approx 1-\frac{1}{2}{D}_{FS}^2$

比较两边的二阶项，我们得到：

$$\frac{1}{2}{D}_{FS}^2\approx 2{\sigma }^2{T}_{WS}^2⟹D_{FS}\approx 2\sigma |T_{WS}|$$

E.4 物理结论

这一推导严格证明了正文中的核心几何命题：

FS 距离 $\approx$ 带宽 $\times$ 时间延迟

这揭示了时间延迟的本质：它不是时间轴上的停顿，而是 状态矢量在射影希尔伯特空间中被拉开的距离。

• 如果延迟 $T_{WS}=0$，则 $D_{FS}=0$，状态没有发生几何偏转（除了全局相位）。

• 延迟越大，出射态与入射态在几何上就越“正交“。

这也为 “延迟-保真度权衡” 提供了数学基础：你无法在获得巨大时间延迟的同时，保持量子态的完美保真度。因为获得延迟（$T_{WS}$）本身就意味着你必须在几何上远离出发点（$D_{FS}$ 增大，重叠 $V$ 下降）。这是几何学强加给信号处理的铁律。