1.2 Imaginary is Orthogonal

“If the universe were merely an exponential function, it would have long since self-destructed. That unassuming imaginary number $i$ in the exponent is physics’ greatest brake pad. It forcibly twists the direction of growth, taming a destined collapse into an eternally elegant rotation.”

In the previous section, we praised the compound interest mechanism of $e$. It revealed that the universe is a “self-driven” system. But if this were the complete truth, we would face a great trouble.

Pure exponential growth $e^t$ is extremely dangerous.

If the Hamiltonian $H$ were merely a real number, then the Schrödinger equation $|\psi (t)⟩=e^{-Ht}|\psi (0)⟩$ would describe not waves, but decay or explosion. The system’s total budget $c_{FS}$ would be instantly exhausted or expand to infinity. Such a universe could not sustain any stable structure.

To allow “existence” to persist, to allow the “circle” to close, the universe introduced a mysterious geometric correction operator.

This is the imaginary unit $i$.

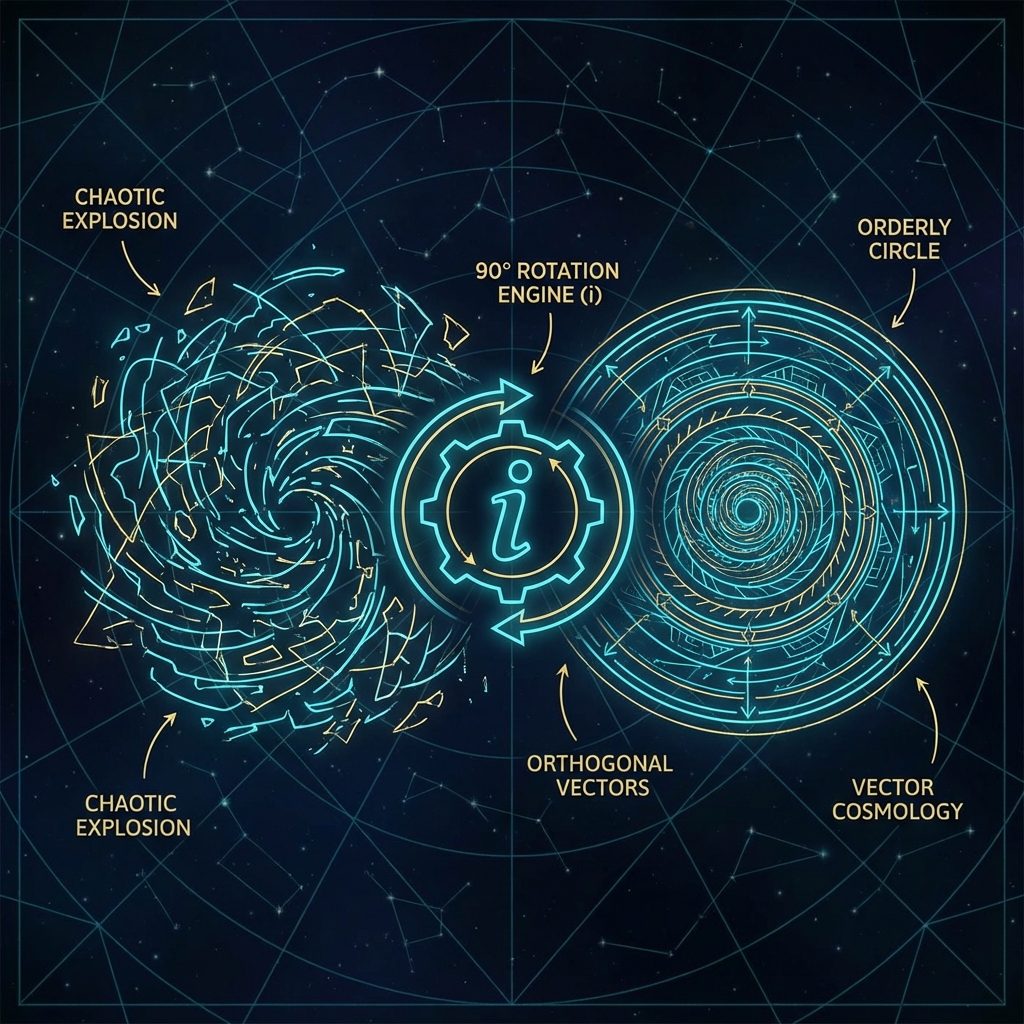
In Vector Cosmology, $i$ is not a ghost imagined by mathematicians; it is the Orthogonal Rotation Operator.

The Magic of 90 Degrees

On the complex plane, multiplying any number by $i$ has the geometric effect of rotating counterclockwise by 90 degrees.

• $1\times i=i$ (rotated to the imaginary axis)

• $i\times i=-1$ (rotated back to the real axis, but in the opposite direction)

This simple geometric operation, when placed into the exponential function $e^{i\theta }$, produces the most profound oscillation in mathematical history: Euler’s formula $e^{i\theta }=\cos \theta +i\sin \theta$.

This tells us: Exponential growth with an imaginary number is no longer a change in quantity, but a change in angle.

Returning to physics. That $-i$ in the Schrödinger equation is actually a “forced steering instruction” at the foundation of the universe.

$$|\dot{\psi }⟩=-iH|\psi ⟩$$

This means: The rate of change of the state vector ($|\dot{\psi }⟩$) must always remain perpendicular (orthogonal) to the current state vector ($|\psi ⟩$).

• If the rate of change is parallel to the state (without $i$), the vector will lengthen or shorten (modulus changes).

• If the rate of change is perpendicular to the state (with $i$), the length of the vector remains unchanged, only the direction shifts.

This is the geometric essence of Unitarity. $i$ is the guardian of conservation laws. It guarantees that no matter how large the Hamiltonian $H$, no matter how intense the evolution, the modulus of the global vector $|\Psi ⟩$ is forever locked at 1.

Vibration is the Projection of Rotation

This perspective completely refreshes our understanding of “waves.”

In classical physics, we are accustomed to the image of “vibration”: the back-and-forth stretching of a spring, the up-and-down undulation of water waves. This is a linear, real-number oscillation.

But in quantum mechanics, the universe does not vibrate; the universe only rotates.

When we see a particle exhibiting sinusoidal wave properties $\sin (kx-\omega t)$, we are actually seeing the projection of a high-dimensional complex spiral onto the real axis.

• That particle is not really “shaking” there.

• Its wave function vector performs a perfect, uniform circular motion in complex space.

As we stated in the first book, FS geometry does not distinguish between “motion” and “rest,” only between “rotation.”

All energy $E$ is essentially angular velocity. All physical evolution is phase rotation driven by $e^{-iHt}$.

The reason we perceive the world as full of waves and cycles is because we live on the side of that rotating vector.

The Game of Conservation and Growth

At this point, we finally see the division of labor between $e$ and $i$.

• $e$ (exponential mechanism): Provides the “self-driving” power. It ensures that evolution at every moment is based on the state of the previous moment, endowing time with continuity.

• $i$ (imaginary mechanism): Provides the “orthogonality” constraint. It forces this driving power to do no work (not changing modulus), only changing direction.

Without $e$, the universe is stagnant water.

Without $i$, the universe is a brief explosion.

Only when the two combine do we obtain that perfect great circle that “circles without exhaustion”.

In the second book, we discussed “spirals” and “dimensional inflation.” In that picture, the rule of imaginary $i$ seems to have loosened slightly (or rather, $H$ acquired a tiny non-Hermitian imaginary part), causing rotation to become a logarithmic spiral $e^{(\lambda +i\omega )t}$.

But even in such wild ascension, the rotation represented by $i$ remains the main theme, and the growth represented by $\lambda$ is merely the accompaniment.

Conclusion: The Truth of Perpendicularity

So, the imaginary is not imaginary. It is the hardest geometric entity in the universe.

It is that wall that blocks the abyss of infinite expansion, forcing time to curve into a ring.

When we understand the orthogonal nature of $i$, we understand why quantum mechanics must be complex. Because only in complex space can “change” occur without destroying “existence” (modulus conservation).

Now, we have mastered the engine of evolution ($e$) and the steering wheel ($i$). The next question is: Where does this engine drive the vector?

Since the universe does not choose a single path, since the wave function spreads throughout space, how do these countless possible trajectories converge into the single history we observe?

This leads to the theme of the next chapter: Path Integral. We will see that the exponential of $e$ not only describes a single rotation, but also describes the sum of all possible histories.