附录 C：李代数与指数映射 (Appendix C: Lie Algebras and the Exponential Map)

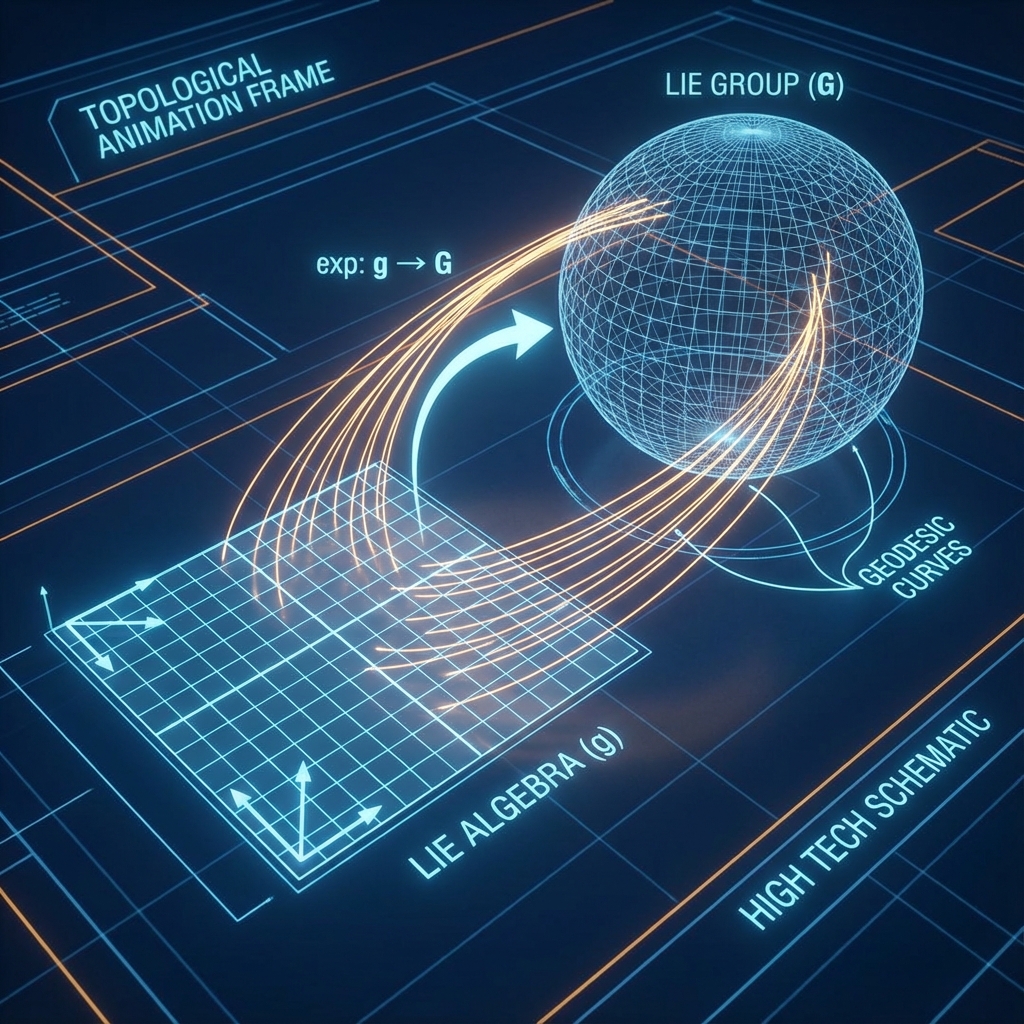
在《矢量宇宙论 III》的第二卷“生成元“中，我们将哈密顿量 $H$ 描述为宇宙演化的“种子“，将 $e$ 描述为将这颗种子展开为时间长河的“机器“。这一物理图像背后的数学结构，是现代数学中最为宏伟的大厦之一——李群与李代数 (Lie Groups and Lie Algebras)。

本附录将提供这一结构的严谨数学描述。我们将证明，为什么任何连续的对称性（如时间的平移、空间的旋转）都必然由一个无穷小的“切矢量“（生成元）通过指数映射 $e^X$ 来生成。这是“导数即本体“的数学铁证。

C.1 弯曲的群与平直的代数

物理学中的对称操作通常构成一个 李群 (Lie Group, $G$)。例如，所有可能的空间旋转构成了 $SO(3)$ 群，所有的时间平移构成了 $T(1)$ 群（同构于实数轴 $\mathbb{R}$）。李群是一个 光滑流形，它既是群（可以运算），又是空间（可以求导）。

然而，李群通常是弯曲的、非线性的（就像地球表面）。直接研究它很困难。

为了简化问题，数学家索福斯·李 (Sophus Lie) 发现了一个天才的方法：只研究群在单位元 $e$（Identity，即“不操作“）处的 切空间 (Tangent Space)。

这个切空间被称为 李代数 (Lie Algebra, $\mathfrak{g}$)。

• $\mathfrak{g}$ 是线性的：它是一个向量空间。你可以把生成元相加、数乘。

• $\mathfrak{g}$ 是无穷小的：它代表了群元素在“刚刚开始变化“那一瞬间的趋势。

C.2 指数映射：连接两界的桥梁

如何从无穷小的切空间 $\mathfrak{g}$ 回到宏大的群流形 $G$？

这就需要 指数映射 (Exponential Map)：

$$\exp :\mathfrak{g}\to G$$

对于矩阵李群（物理学中大多如此），这个映射就是我们在高等代数中学到的矩阵指数：

$$e^X=\sum _{k=0}^{\infty }\frac{X^k}{k!}=I+X+\frac{1}{2}{X}^2+\dots$$

定理：对于李代数中的任意元素 $X\in \mathfrak{g}$，$e^{tX}$ (其中 $t\in \mathbb{R}$) 构成李群 $G$ 中的一个 单参数子群 (One-Parameter Subgroup)。

$$g(t)=e^{tX}$$

满足 $g(t+s)=g(t)g(s)$。

物理意义：

• $X$ (生成元)：不仅是一个切矢量，它是一条 测地线 (Geodesic) 的“初速度“。

• $e^{tX}$ (轨道)：就是这股初速度在流形上“滑行“出的完整轨迹。

宇宙不需要记住整条轨迹，宇宙只需要记住起点和初速度 $X$（即哈密顿量）。

C.3 哈密顿量作为切矢量

在量子力学中，幺正演化群 $U(t)$ 是一个李群（$U(N)$ 或无限维幺正群）。

薛定谔方程定义了它的切矢量：

$$\frac{d}{dt}U(t){|}_{t=0}=-iH$$

这里的 $-iH$ 就是李代数元素。

• 因为 $U$ 是幺正的 ($U^{†}U=I$)，所以 $-iH$ 必须是 反厄米 (Anti-Hermitian) 的。

• 这意味着 $H$ 必须是 厄米 (Hermitian) 的（物理可观测量的要求）。

所以，物理学家所说的“能量算符 $H$“，在几何学家的眼中，就是一个位于幺正群单位元切空间里的 切矢量。

它定义了宇宙演化的“方向“。

C.4 为什么必须是 $e$？

为什么演化算符非得是 $e^{-iHt}$？为什么不能是 $2^{-iHt}$ 或者 $\sin (Ht)$？

这是一个关于 同态 (Homomorphism) 的唯一性定理。

我们要求时间演化满足两个基本条件：

1. 连续性：$U(t)$ 随 $t$ 平滑变化。

2. 半群性质：$U(t_1+t_2)=U(t_1)U(t_2)$（先演化 $t_1$ 再演化 $t_2$，等于直接演化 $t_1+t_2$）。

数学定理指出：满足上述条件的唯一非平凡连续函数形式，就是指数函数。

这从根本上解释了为什么自然界选择了 $e$。

$e$ 不是一个随意的常数，$e$ 是 “连续性” 与 “因果累积性” 在逻辑上必然导致的数学形式。只要我们承认时间是连续流逝的，且过去的历史会累积到当下，宇宙就必须通过 $e$ 来驱动自己。