第三篇：全息动力学 (Part III: Holographic Dynamics)

第五章 欧米伽作用量原理 (The Omega Action Principle)

在前两篇中，我们构建了宇宙的静态本体（希尔伯特空间矢量 $|\Omega ⟩$）和离散时空背景（欧米伽网格）。第四章证明了在微观尺度上，离散的量子元胞自动机自然涌现出满足狄拉克方程的波函数。然而，要建立一个完备的统一场论，我们必须解释宏观物理定律的动力学起源：为什么粒子遵循最小作用量原理？为什么引力场方程具有特定的形式？

本章提出 欧米伽作用量 (The Omega Action)，记为 $S_{\Omega }$。我们主张，物理学中著名的 最小作用量原理 (Principle of Least Action)，其本质是计算理论中的 “最小计算复杂度原理” (Principle of Least Computational Complexity)。宇宙是一个寻求以最低比特成本处理最大量信息的优化算法。我们将证明，通过最小化费雪信息 (Fisher Information) 并施加拓扑约束，可以推导出标准模型和广义相对论的核心拉格朗日量。

5.1 费雪信息拉格朗日量 (Fisher Information Lagrangian)

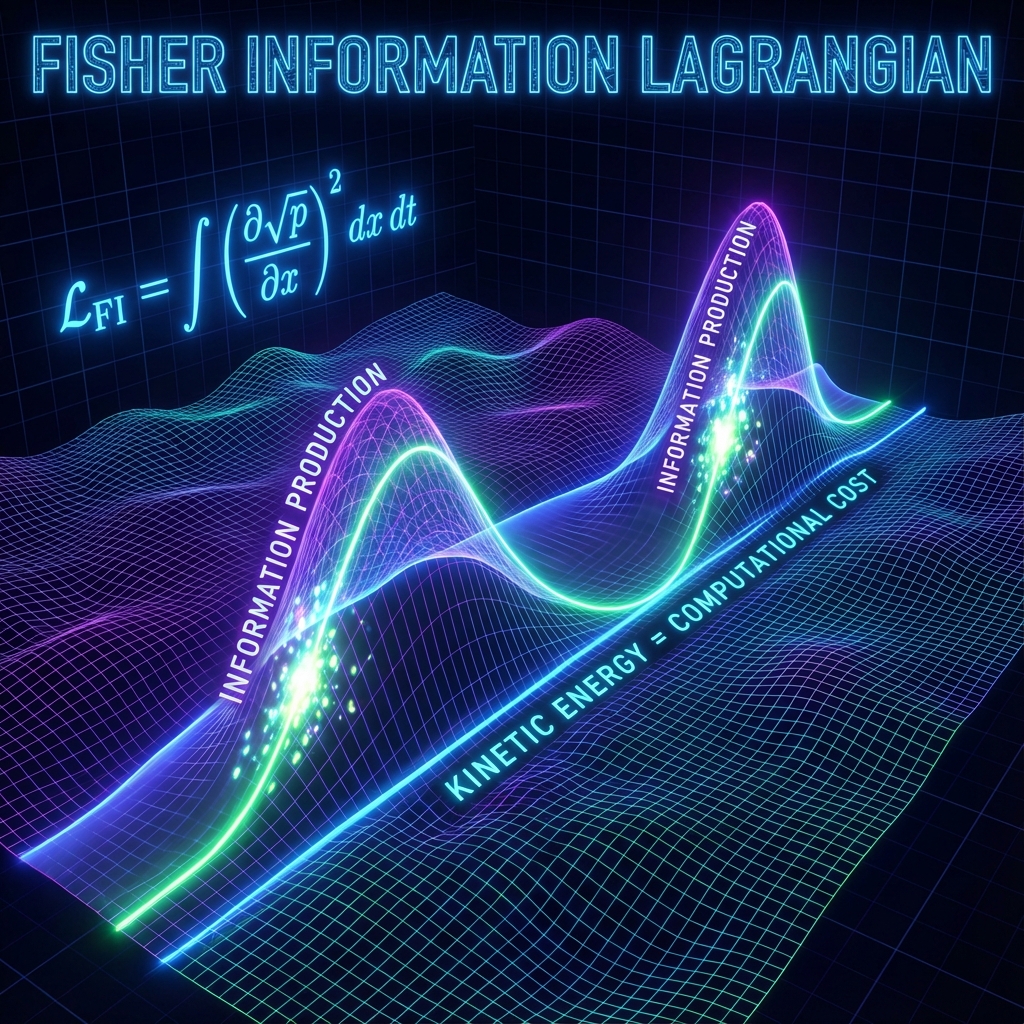
在经典力学中，拉格朗日量通常被定义为动能减去势能 ($T-V$)。这种定义虽然在数学上有效，但在本体论上是任意的。为何动能采取二次型？为何势能由位置决定？在 信息几何 (Information Geometry) 的框架下，这些物理量获得了更深层的解释：它们是概率分布流形上的几何度量。

5.1.1 物理实在作为概率分布

回顾第一篇的公理，物质场 $\psi (x)$ 本质上是欧米伽网格上的概率幅分布。根据 B. Roy Frieden 的开创性工作，物理测量的本质是从系统中提取信息。描述这种提取过程效率的度量是 费雪信息 (Fisher Information)。

对于一个参数化为时空坐标 $x^{\mu }$ 的概率密度函数 $p(x)=|\psi (x){|}^2$，其费雪信息 $I$ 定义为：

$$I=\int \frac{1}{p(x)}\left(\frac{\partial p}{\partial x^{\mu }}\right)\left(\frac{\partial p}{\partial x_{\mu }}\right)d^{4}x$$

这量化了概率分布随位置变化的剧烈程度。如果分布极其平坦（无序），信息量极低，梯度为零；如果分布高度局域化（有序），信息量极高。

在欧米伽理论中，我们将这一概念推广到复振幅 $\psi$，构建 欧米伽信息流密度 (Omega Information Flux Density)：

$$J_{\mu }=\frac{\partial \psi }{\partial x^{\mu }}$$

则对应的费雪信息量 $I_{\Omega }$ 正比于梯度的模方：

$$I_{\Omega }\propto \int g^{\mu \nu }({\nabla }_{\mu }\psi {)}^{†}({\nabla }_{\nu }\psi )\sqrt{-g}{d}^{4}x$$

5.1.2 动能项的推导

我们观察到，$I_{\Omega }$ 的形式与标量场或旋量场的 动能项 (Kinetic Term) 惊人地一致。这并非巧合。

定理 5.1 (信息-动能等价原理)： 任何物理场的动能项 ${\mathcal{L}}_{kin}$，在本质上都是该场在时空流形上传播时的 费雪信息产生率 (Fisher Information Production Rate)。最小化作用量 $S\sim \int {\mathcal{L}}_{kin}$ 等价于要求系统在演化过程中以最平滑（信息损失最小）的方式传递概率幅。

对于自旋-1/2 的狄拉克场 $\Psi$，我们引入协变导数 ${\mathcal{D}}_{\mu }$ 以包含规范连接（即第 2 章导出的 $SU(N)$ 几何）。此时，基于信息的拉格朗日密度 ${\mathcal{L}}_{\text{Info}}$ 为：

$${\mathcal{L}}_{\text{Info}}=\bar{\Psi }i{\gamma }^{\mu }{\mathcal{D}}_{\mu }\Psi$$

这一项代表了 “软硬件交互成本”：即波函数 $\Psi$（软件）在弯曲时空背景 $g_{\mu \nu }$（硬件）上流动时所消耗的计算带宽。

5.1.3 拓扑势与几何约束

如果宇宙仅包含 ${\mathcal{L}}_{\text{Info}}$，系统将趋向于最大熵的均匀分布（热寂）。为了产生结构，必须引入约束项。在标准模型中，这是通过人为引入势能项 $V(\varphi )$ 实现的。在欧米伽理论中，势能项源自 拓扑几何约束。

回顾 1.2 节，宇宙必须沿着斐波那契螺旋演化。任何偏离这一 黄金轨道 (Golden Trajectory) 的状态都会产生巨大的“几何张力“。我们将这种张力形式化为 拓扑势 (Topological Potential) ${\mathcal{V}}_{\text{Topo}}$。

$${\mathcal{V}}_{\text{Topo}}(\Psi )=\lambda {\left(|\Psi {|}^2-{\rho }_{\varphi }(\tau )\right)}^2$$

其中 ${\rho }_{\varphi }(\tau )\propto {\varphi }^{2\tau }$ 是由黄金幺正算符决定的理想信息密度。

• 当系统的局部信息密度 $|\Psi {|}^2$ 匹配宇宙背景的斐波那契增长率时，势能为零，系统处于 共振态。
• 当出现偏差（例如形成过高密度的黑洞，或过低密度的空洞）时，${\mathcal{V}}_{\text{Topo}}$ 急剧增加。

此外，为了打破时间反演对称性（见 2.1 节），我们必须引入一个 手性约束项 (Chiral Term)，通常表现为拓扑陈-西蒙斯项 (Chern-Simons Term)：

$${\mathcal{L}}_{\text{Chiral}}=\kappa {ϵ}^{\mu \nu \rho \sigma }{F}_{\mu \nu }{F}_{\rho \sigma }$$

这锁定了时间箭头的方向。

5.1.4 欧米伽总作用量

综合上述各项，我们写出支配交互式计算宇宙的终极公式—— 欧米伽作用量：

$$S_{\Omega }={\int }_{\mathcal{M}}{d}^{4}x\sqrt{-g}\left[\underset{\text{几何熵 (硬件)}}{\underbrace{\frac{R}{16\pi G_{\text{eff}}}}}+\underset{\text{费雪信息 (软件)}}{\underbrace{\bar{\Psi }i{\gamma }^{\mu }{\mathcal{D}}_{\mu }\Psi }}-\underset{\text{斐波那契约束}}{\underbrace{\lambda (|\Psi {|}^2-{\varphi }^{\tau }{)}^2}}+\underset{\text{手性}}{\underbrace{{\mathcal{L}}_{\text{Chiral}}}}\right]$$

这个公式的物理意义可以重新解读为 最小计算复杂度原理：

1. 第一项 ($R$)：最小化时空网格的弯曲，即维持硬件架构的平整性。
2. 第二项 (${\mathcal{D}}_{\mu }$)：最小化信息流动的梯度，即寻找最优传输路径。
3. 第三项 ($\varphi$)：强制系统输出与黄金分割增长率同步，即满足系统时钟频率。
4. 第四项 (Chiral)：强制运算过程的因果序。

物理学中的“力“，无论是引力、电磁力还是强力，在这个框架下都是为了满足上述 优化算法 而产生的 拉格朗日乘子 (Lagrange Multipliers)。粒子运动的轨迹，就是宇宙计算机在宏观上找到的“最省力“计算路径。