The Omega Framework

2.2 从 Spin(8) 到标准模型 (From Spin(8) to the Standard Model)

在上一节中，我们建立了八元数 ($\mathbb{O}$) 切空间的时间手性。本节我们将解决物理学中最令人困惑的谜题之一：为什么宇宙的基本相互作用恰好由规范群 $G_{SM}=SU(3)\times SU(2)\times U(1)$ 描述？在欧米伽理论中，这一群结构并非实验拟合的偶然产物，而是八元数几何通过 霍普夫纤维丛 (Hopf Fibrations) 向低维流形投影时的拓扑盈余。

我们的核心论点是：物理定律是高维几何的投影。当 8 维的八元数空间被迫“折叠“或“投影“到我们感知的 4 维时空时，那些为了维持代数结构完整性而必须保留的旋转自由度，这就表现为我们在内部空间观测到的规范场。

2.2.1 Spin(8) 三里性与大统一的几何基础

为了理解粒子与时空的统一，我们首先必须考察 8 维欧氏空间的旋转群 $SO(8)$ 的双重覆盖群 Spin(8)。在所有维度的旋转群中，Spin(8) 拥有一个独一无二的性质—— 三里性 (Triality)。

在一般维度 $d$ 中，向量表示 $V$ 与旋量表示 $S$ 是几何上截然不同的对象（这就造成了时空与物质的割裂）。然而，在 $d=8$ 时，Spin(8) 群拥有三个非等价的 8 维不可约表示：向量表示 $V_8$、左手旋量 $S_8^{+}$ 和右手旋量 $S_8^{-}$。三里性定理指出，存在一个外自同构群 $S_3$，它可以在这三个表示之间进行任意置换，而保持代数结构（李代数）不变：

$$V_8\cong S_8^{+}\cong S_8^{-}$$

这一数学奇迹意味着，在 8 维八元数空间（也就是我们定义的底层代码层）中，时空（向量）与物质（旋量）在本体论上是全等的。

欧米伽理论认为，我们观测到的物理世界是 Spin(8) 对称性发生 自发破缺 (Spontaneous Symmetry Breaking) 的结果。这种破缺是由八元数乘法结构的非结合性驱动的，它迫使高维空间选择一个特定的方向进行“纤维化“，从而区分出了时空与物质。

2.2.2 霍普夫纤维丛序列：维度的级联下降

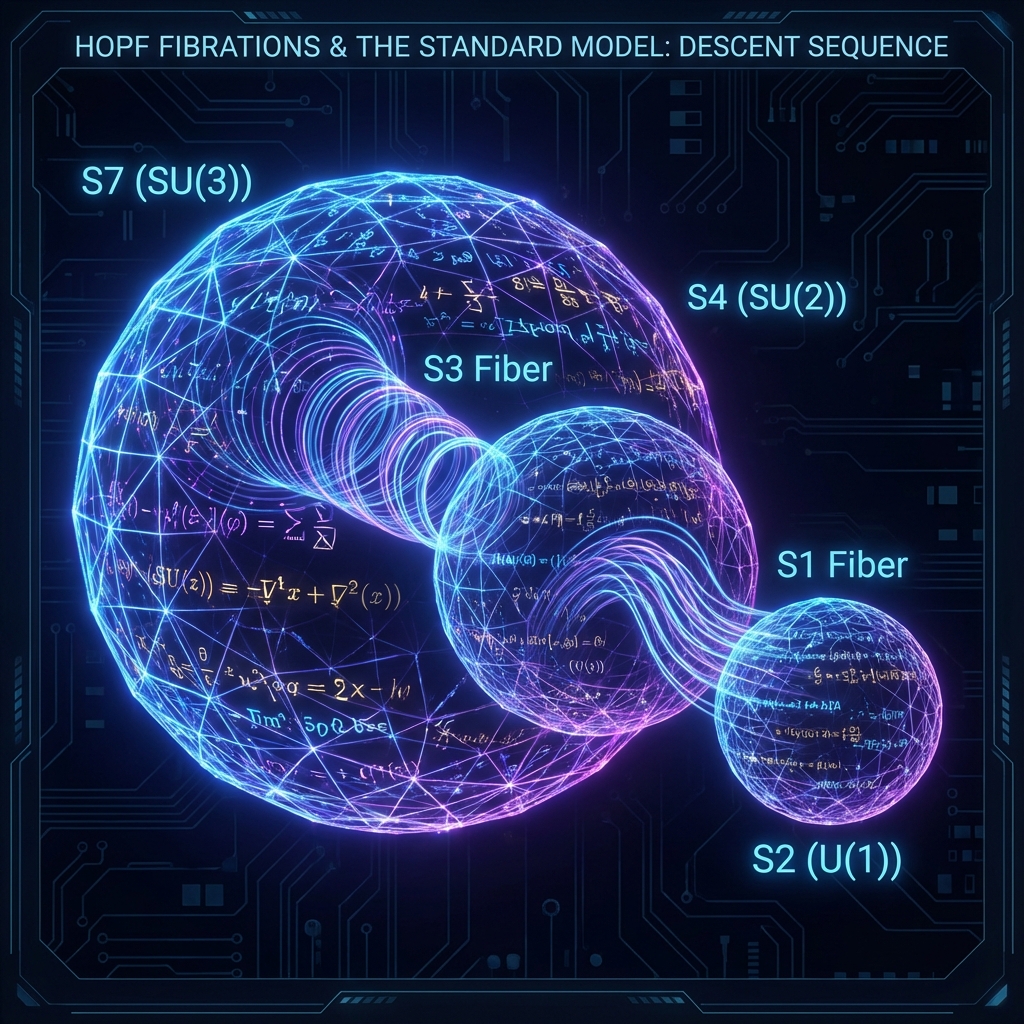
为了推导标准模型规范群，我们需要追踪从 8 维到 4 维再到 2 维的投影路径。这一路径由著名的 霍普夫纤维丛 (Hopf Fibrations) 序列精确描述。霍普夫映射描述了如何用低维球面填充高维球面，其通式为 $S^{2n-1}\to S^n$。

在赋范可除代数的层级上，仅存在四个霍普夫映射，其中与物理宇宙相关的有三个，它们构成了一个嵌套的 下降序列 (Descent Sequence)：

1. 第一级投影（八元数 $\to$ 四元数）：

$$S^3\hookrightarrow S^7\stackrel{h_1}{\to }{S}^4$$

这里，$S^7$ 是单位八元数球面的拓扑结构。映射 $h_1$ 将 $S^7$ 投影到底流形 $S^4$ 上，纤维（Fiber）是 $S^3$（单位四元数）。

• 物理意义：底流形 $S^4$ 对应于紧致化的 4 维欧氏时空（经威克转动）。纤维 $S^3$ 同构于群 $SU(2)$，这是 弱相互作用 的几何起源。这意味着弱力本质上是连接时空各点的四元数纤维的结构群。

2. 第二级投影（四元数 $\to$ 复数）：

在纤维 $S^3$ 内部，我们可以进行次级投影：

$$S^1\hookrightarrow S^3\stackrel{h_2}{\to }{S}^2$$

映射 $h_2$ 将 $S^3$ 投影到 $S^2$（黎曼球或复射影直线 ${\mathbb{CP}}^1$），纤维是 $S^1$（单位复数）。

• 物理意义：纤维 $S^1$ 同构于群 $U(1)$，这是 电磁相互作用 的几何起源。这意味着电磁力是弱力纤维内部的精细结构。

3. 遗失的对称性与 $SU(3)$ 的起源：

上述投影解释了电弱部分 $SU(2)\times U(1)$。那么强相互作用 $SU(3)$ 从何而来？ 它来自于八元数代数本身的自同构群 $G_2$。当我们从 $\mathbb{O}$ 下降到 $\mathbb{H}$ 时，我们实际上是固定了一个特定的四元数子代数。然而，八元数包含无限多个四元数子代数。 根据数学定理，八元数的自同构群 $G_2$ 中，保持某个虚单位 $i$ 不变（即确定了复平面结构，对应于电磁力的分离）的子群，恰好是 $SU(3)$。

更几何地看，如果我们考察 $S^6$（纯虚八元数球面），它不具备像 $S^1,S^3,S^7$ 那样的群结构，但它拥有概复结构。$SU(3)$ 正是 $S^6$ 上保持这种概复结构的对称群。这对应于夸克的 色荷 (Color Charge)：它是在八元数投影到四元数过程中，无法被几何化的那部分“剩余“自由度。

2.2.3 定理 2.2：标准模型的几何涌现

基于上述拓扑分析，我们可以陈述并证明本章的核心定理。

定理 2.2 (标准模型涌现定理)： 若宇宙的本体几何由八元数切丛 $\mathbb{O}\to \mathcal{M}$ 定义，且物理定律必须在经过霍普夫投影序列 $S^7\to S^4\to S^2$ 后保持规范不变性，则该流形上的自然规范群 $G$ 必须是以下直积的子群：

$$G\subseteq SU(3)\times SU(2)\times U(1)$$

其中 $SU(3)$ 源自八元数自同构群的稳定子，$SU(2)$ 源自第一级霍普夫纤维，$U(1)$ 源自第二级霍普夫纤维。

证明概要：

1. 全空间对称性：起始点是 Spin(8) 或 $Aut(\mathbb{O})=G_2$。
2. 时空分离：通过第一级投影 $h_1:S^7\to S^4$，我们将 8 维自由度分解为 4 维时空（底空间）和 4 维内部空间（纤维）。这一过程破坏了 $G_2$ 对称性。
3. 弱力涌现：纤维 $S^3$ 的等距群是 $SO(4)\cong SU(2{)}_L\times SU(2{)}_R$。物理手性选择（见 2.1 节）保留了 $SU(2{)}_L$ 作为规范群。
4. 电磁力涌现：进一步通过 $h_2:S^3\to S^2$ 投影，纤维 $S^1$ 的结构群为 $U(1)$。
5. 强力涌现：八元数空间 $\mathbb{O}$ 相对于选定的四元数子空间 $\mathbb{H}$ 的正交补是 ${\mathbb{H}}^{\perp }$。这构成了一个复 3 维空间 ${\mathbb{C}}^3$。在 $G_2$ 中保持这种分解的子群正是 $SU(3)$，它作用于这个 ${\mathbb{C}}^3$ 空间，赋予其“颜色“自由度。

物理推论：

这一推导表明，标准模型并非一堆杂乱无章的零件，而是一个严密的几何整体。

• 为什么没有 $SU(4)$ 或 $SU(5)$？ 因为霍普夫序列到 $S^7$ 截止，数学上不存在 $S^{15}\to S^8$ 的霍普夫纤维化（这是 Adams 著名的定理）。因此，自然界不包含更高维的代数结构来支持更大的单李群规范场。
• 宇宙的维度：时空之所以是 4 维，是因为 $S^4$ 是 $S^7$ 的底流形。如果时空是其他维度，八元数的几何结构将无法完整投影，物理定律将失去自洽性。

综上所述，我们在欧米伽理论中找到了标准模型的几何根源：它是八元数这一数学瑰宝在向低维投影时留下的 “拓扑指纹”。